九州大学 理学研究院 理学府 理学部

解けない方程式と解ける方程式

　「方程式」と聞くと、解き方に定石があって、それに従って式変形をすると答えが見つかる、というイメージを持たれている方は多いかと思います。しかし、今回の主題である非線形微分方程式 “non-linear differential equation” には、厳密な解を見つける汎用的な方法はないことが知られています。こういった方程式は、自然界を記述する様々な法則として姿を表すため、工学などの目的で解を知りたい場合は、数値計算などによって近似的な解を得るしかありません。しかし、そんな非線形微分方程式の中には、時として技巧的な式変形を駆使することで、奇跡的に解を具体的な数式で表現できるものがあり、それらは可積分系 “integrable systems” ^[2] と呼ばれています。解ける非線形微分方程式を調べることで見えてくるものとは何なのでしょうか？

曲線に現れる可積分系

　微分や積分を使って幾何学的な対象を研究する、微分幾何学 “differential geometry” と呼ばれる数学の一分野があります。その分野に登場する非線形微分方程式のいくつかは可積分系であることが知られています。そこで、ここでは可積分系が現れる曲線の等周変形 “isoperimetric deformation” 問題、すなわち、長さが変わらない曲線の変形について考えてみます。

　さらに、ここでは三次元の空間内にある曲線について考えます。曲線の変形を考えるための準備として、最初にその曲線がどのような曲線かを指定する必要があります。まず、曲線上の各点では、図1のように、曲線の接線 “tangent” 方向と 2 つの垂直方向 (法線 “normal” 、従 (陪) 法線 “binormal” ) を定めることができます。また、これら 3 つの方向^[3] は、曲線に沿って向きが変わっていきます。その向きの変化を表す量として、曲率 “curvature” (曲線の曲がり具合を表す) と捩率 “torsion” (曲線のねじれ具合を表す) を定義します。曲線に沿った向きの変化を数学的に表現するために微分^[4] が必要となり、この関係を表す公式がフレネ・セレの公式 “Frenet–Serret formulas” です。こうして、どんな曲線を考えるのかを指定することができました。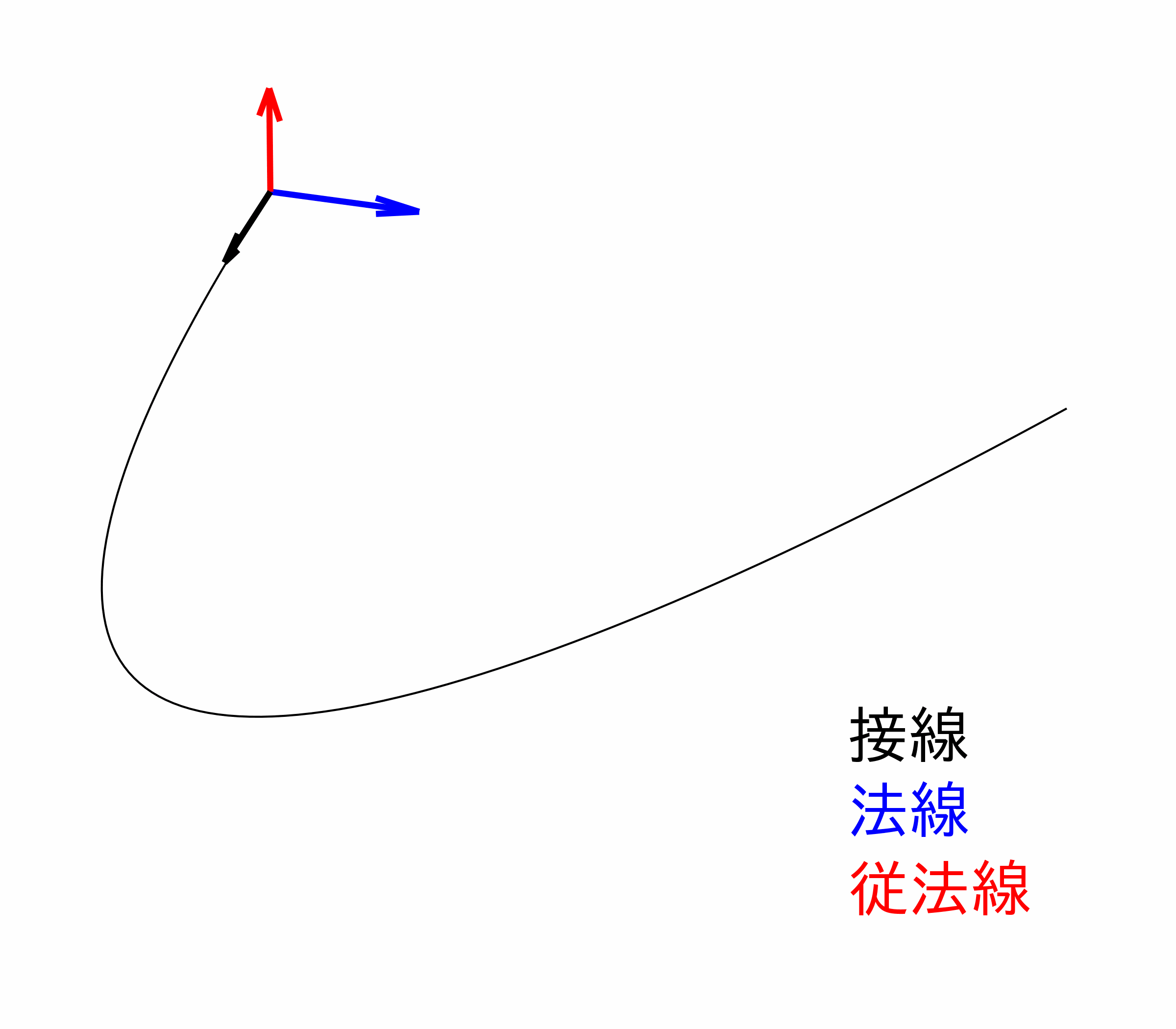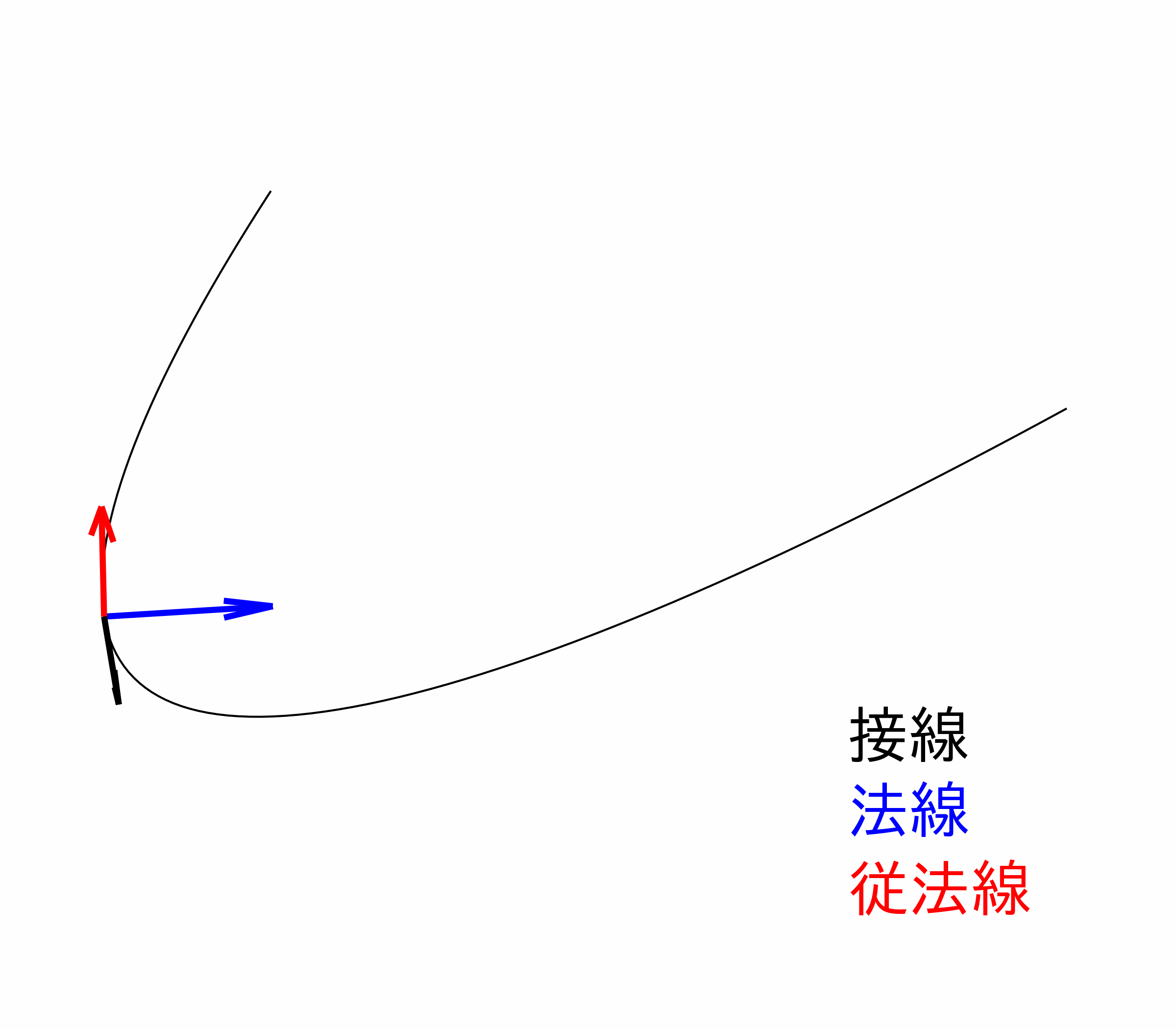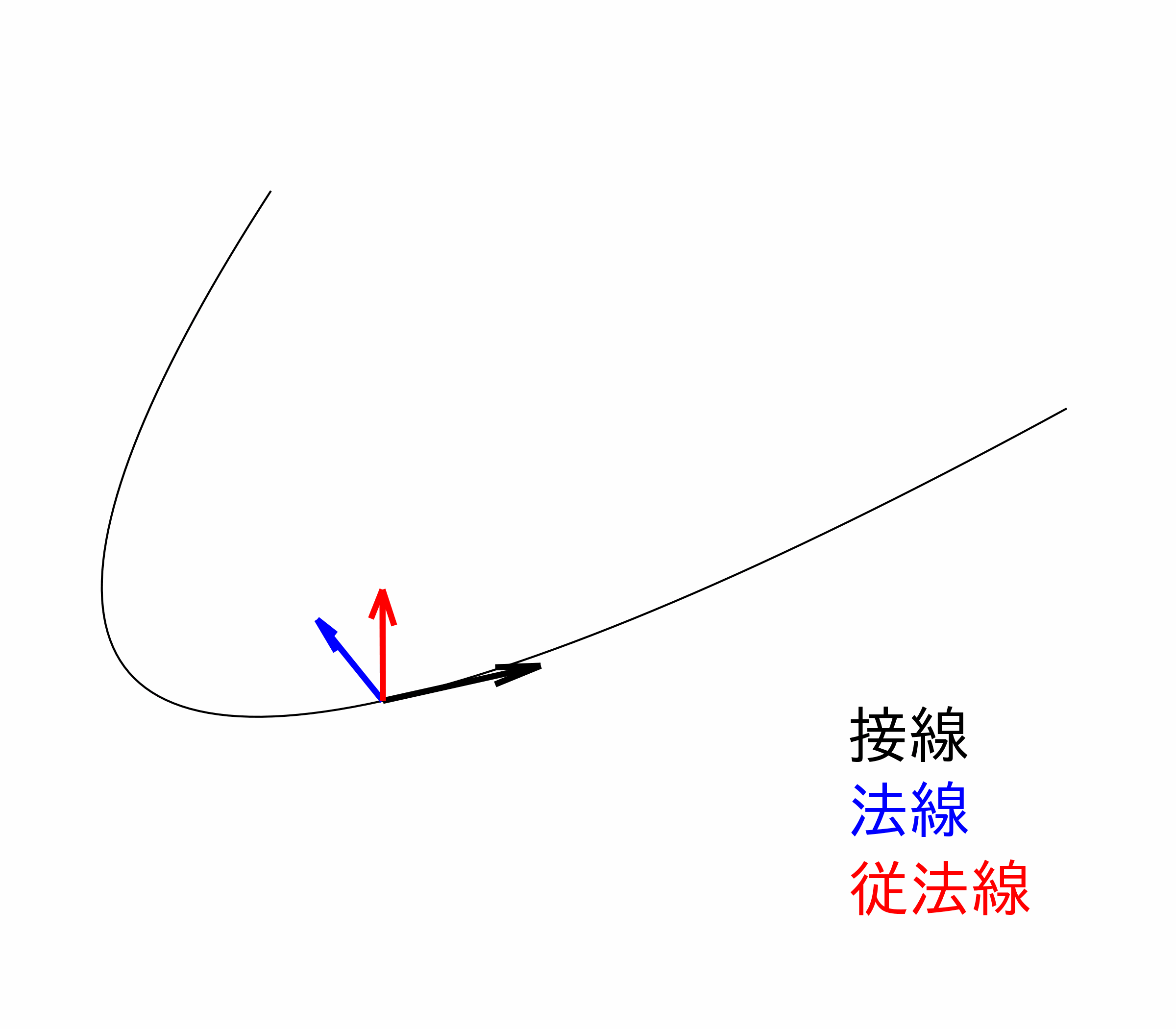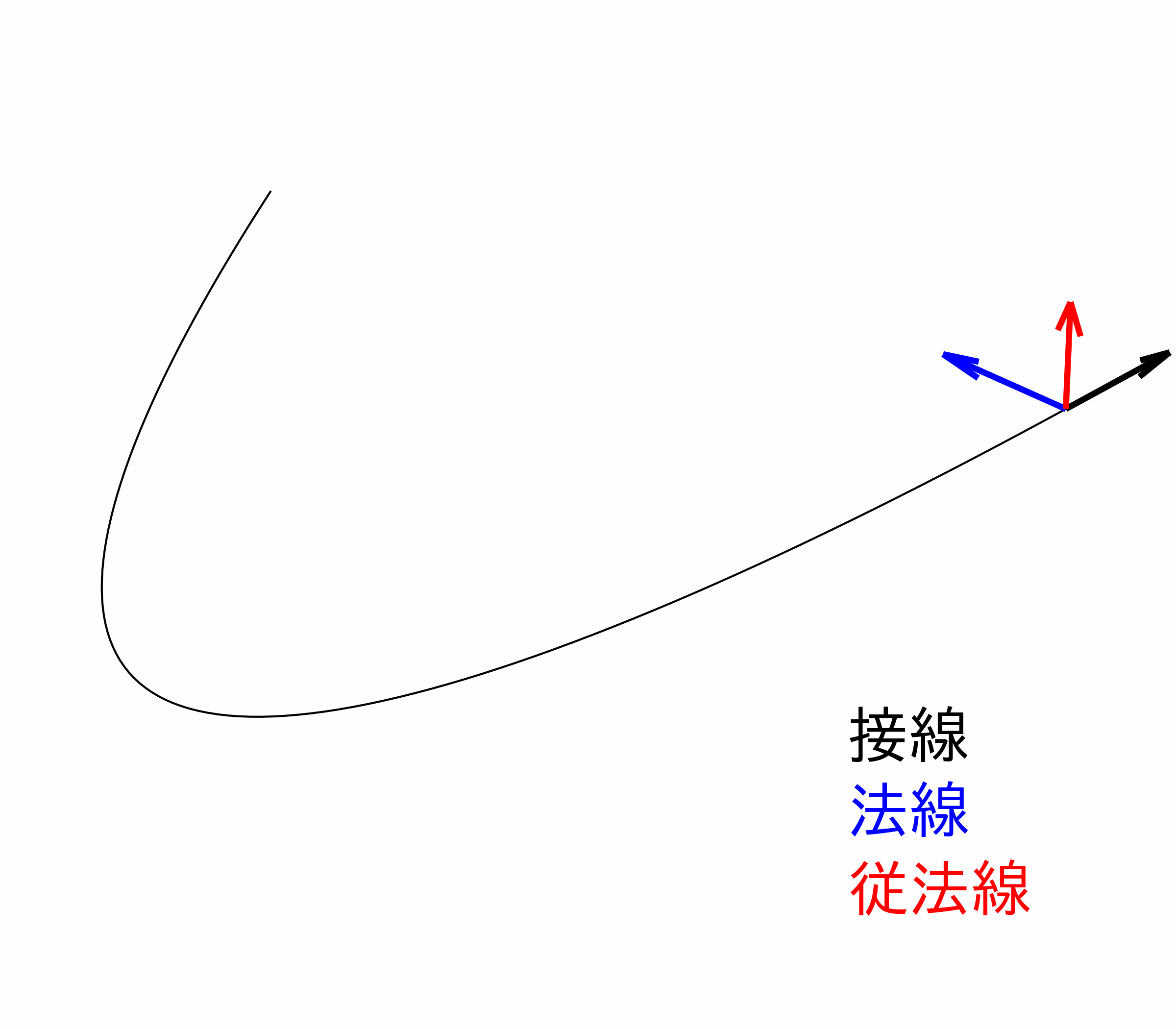

　いよいよ曲線の変形を考えます。曲線が変形すると、それに伴って接線の方向などは変化するはずです。この変化も再び微分^[5] を用いて表すことになります。これに加えて、曲線の長さは変えないように変形するという条件を課すと、曲率は mKdV 方程式 “modified Korteweg–de Vries” (変形 KdV 方程式) という非線形な微分方程式をみたすことがわかります。この方程式は有名な可積分系の一つであり、一つの解として楕円テータ関数 “elliptic theta functions” と呼ばれる特殊関数 “special functions” ^[6] で表されるものがあって、それがカライドサイクルの研究で重要な役割を果たします。

連続から離散へ

　ここまでの話は、なめらかな曲線が長さを変えずに変形すれば、それを表す方程式は可積分系であるというものでした。実は、なめらかに変化できると考えて導出した方程式が可積分系ならば、その可積分系としての性質を保ったまま離散化することが可能で^[7] 、例えば両者の解を表す数式が似ているようにすることができるといわれています。ここで、「離散化」とはどういうことかというと、例えば、図2のように、なめらかな曲線ではなくて折線を考える^[8]、というようなことです。すなわち、長さが変わらない折線の変形を表す方程式も可積分系であり、なめらかな曲線の等周変形の場合と同じように楕円テータ関数を用いて表現される解をもつ、ということになります。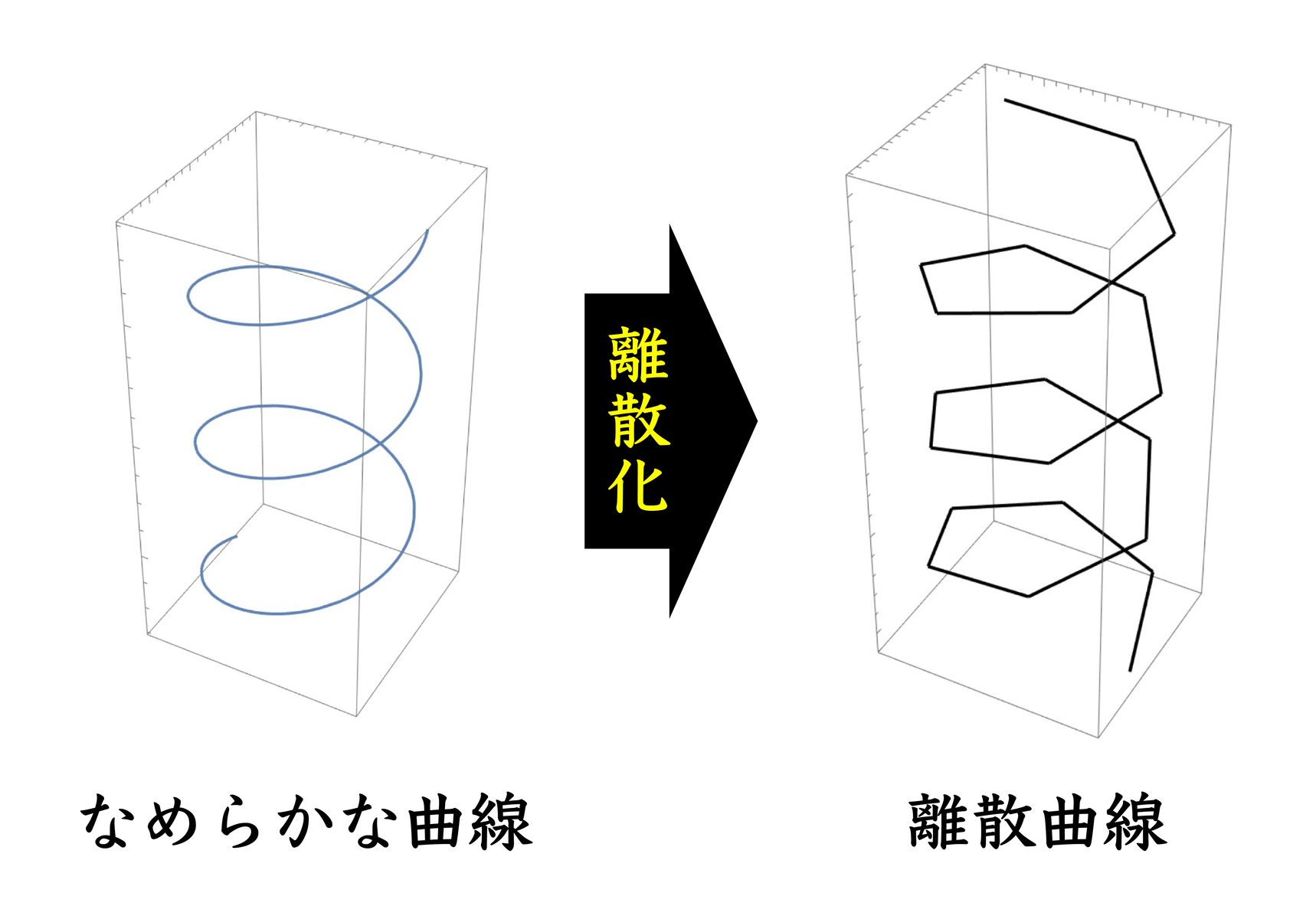

カライドサイクルも離散曲線の変形

　カライドサイクル “kaleidocycle” (図3) という簡単な工作で作れて、クルクルと回るおもちゃ^[9] をご存知でしょうか？なぜ急にそんな話をと思われるかもしれませんが、このカライドサイクルは、先ほどお話した離散化された曲線の変形と深く関係しています。

　図4 をご覧ください。カライドサイクルは合同な四面体が連なった構造をしており、それらをつなぐ蝶番の部分が、赤線で示されています。この蝶番の中点を結ぶ線 (図4 の青線) に注目すると、カライドサイクルを離散化された曲線だとみなすことができます。このとき、蝶番の部分は離散化された曲線の従法線に対応します。図5 の動画は、カライドサイクルがクルクルと回っている間の蝶番の部分の動きを見やすくしたものです。この動画をよく見ると、隣り合う蝶番部分がなす角度は、クルクルと回っている間、常に直角であることが分かります。この角度は離散化された曲線のねじれ具合と関係しているため、カライドサイクルがクルクルと回る運動は、長さと捩率が変化しない離散化された曲線の変形だととらえることができます。このことから、カライドサイクルの動きを表す方程式も可積分系で、解は楕円テータ関数を用いて表現できることが証明できます。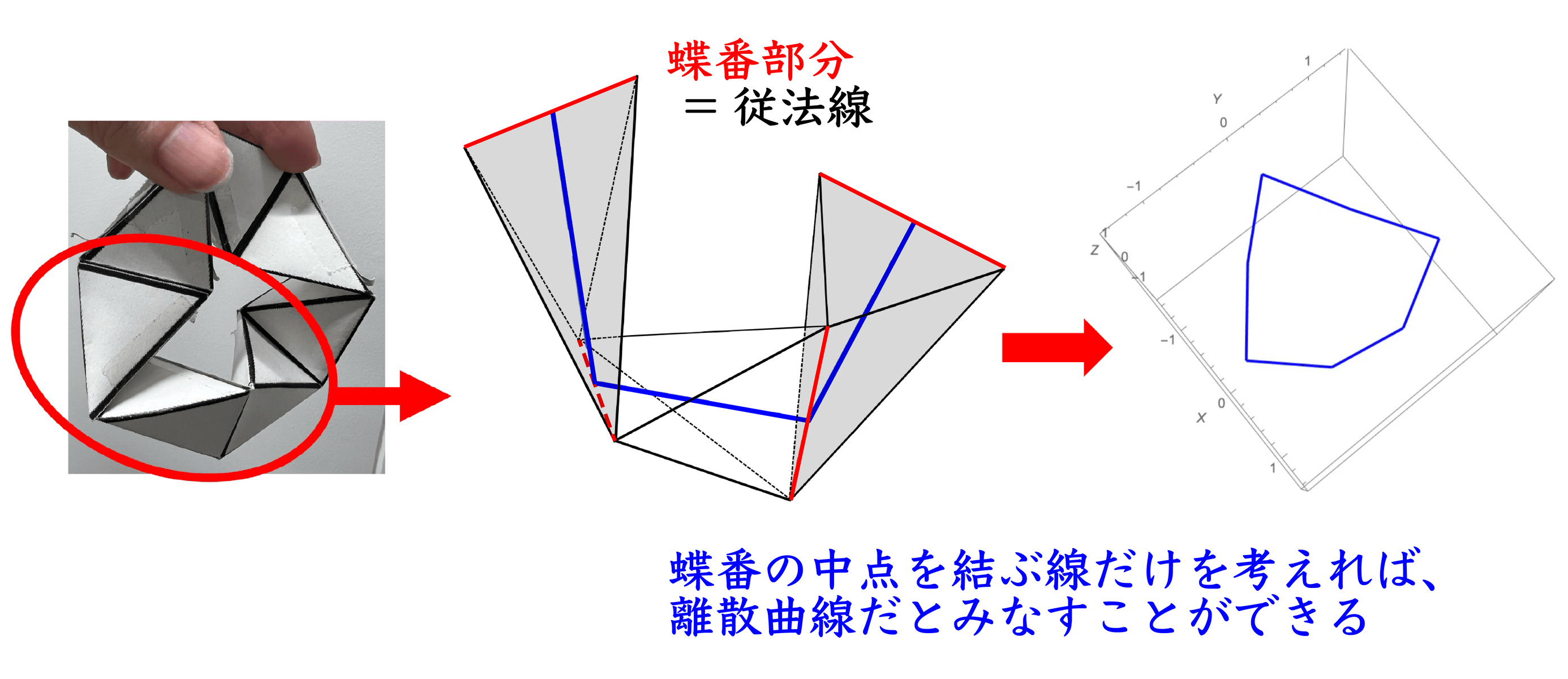

カライドサイクルの動きを離散曲線として考える場合は、数学的な問題が生じないように、接線・法線・従法線の組を標準的な定義から修正する必要がありました。この部分が、本研究で工夫した点の一つです。

まとめと展望

　今回の研究で、カライドサイクルがクルクルと回る動きを楕円テータ関数を用いて表現することができました。このように、解を具体的な数式で書くご利益の一つが、保存量の存在を知ることができることです。保存量 “invariant” とは、考えている対象の変形や運動の間、ずっと一定な物理量のことで、その問題を深く理解する上で非常に重要になります。しかし、カライドサイクルのクルクルと回る動きに関する保存量の中には、数値計算では一定値になりそうだと確認されていても、数学的な証明は未だできていないものがあるそうです。これらの証明に、楕円テータ関数がもつ豊かな性質が役に立つだろうと重富さんは予想しています。

　また、四面体の数や形、ねじれ具合を変えることで、様々な種類のカライドサイクルを作ることができます。特に、メビウスの輪のようにひねったメビウス・ “Möbius” カライドサイクル “kaleidocycle” は、四面体の数を増やしても回転以外の変形ができないという他のカライドサイクルにはない面白い性質をもつことが知られています。加えて、このメビウス・カライドサイクルを作るためには、ひねる回数がある条件を満たしていなければならないということが、マス・フォア・インダストリ研究所の鍛冶 静雄 教授によって示されました。しかし、これらの性質もまた数値計算による予想であり、数学的な証明は未解決です。カライドサイクルは見ていて面白いというだけでなく、工学的にも有用な機構を持ち合わせているため、このような性質の理解の積み重ねが思わぬ技術革新につながるかもしれません。

せっかく生まれてきたのだから、世界の誰も解いたことのないような問題を解きたいという夢があります。

数学には実体がないですが、誰も触れられないからこそ、誰も壊すことができない、永遠に残り続けるものだと考えています。

　さらに、重富さんは、カライドサイクル以外の研究についても開拓していこうと考えているそうです。応用物理や地球科学などに現れる非線形方程式の中には、可積分系という観点から研究されていないものがたくさんありそうです。もしかすると、実は可積分系なのに、そのことに気づかれていない方程式もあるかもしれません。方程式が可積分系だと判明すると、保存量の存在など方程式の背後の多様で明示的な数理構造によって、現象に対して単なるシミュレーション以上の深い理解につながります。

自分の武器は、テータ関数を使いこなせることです。このような武器を増やして、自分にしかできない研究を続けていきたいと考えています。

遊びから始まった共同研究

　重富さんは変わった経歴の持ち主で、学部時代は数学科ではなかったそうです。高校時代は「物理の方が好きだけど、数学の方が得意」という感じで、学部は理学部の地球惑星科学科に入学しました。非線形微分方程式との出会いは、学部時代に宇宙や天文学に憧れて勉強をしていたときのことです。非線形の微分方程式はほとんど解けないけれど、ごくまれに解くことのできる奇跡のような存在があるということを知り、魅力に引き込まれていきました。非線形の微分方程式を解く過程にパズルのような面白さを感じ、物理ではなく物理の背後にある数学の方が好きなんだと気づいたそうです。そこで、思い切って大学院は数理学府に出願し、見事合格しました。

　それから修士、博士と進学して、しばらく時間がたったある日、学部時代の同級生だった地球惑星科学専攻の西脇 瑞紀さんと数年ぶりに会って食事をすることになりました。そこで、お互いの研究の話になったそうです。重富さんは、もともと数学を他分野の研究に応用したいという思いがあり、西脇さんとの会話がきっかけで地球惑星科学の研究にも自分の強みを活かせるかもしれないと考えました。後日、西脇さんにお願いして、普段研究の参考にしている教科書を持ってきてもらいました。それらをペラペラとめくっていると、古典核形成理論のページになにやら見覚えのある級数が書いてあったそうです。これはまさにテータ関数でした。教科書になっている内容は基本的に調べ尽くされているというイメージですが、分野が違えばそうとは限りません。古典核形成理論の中で、テータ関数を用いた研究がどれくらいあるのか調べてみたそうですが、全くなかったそうです。これなら、何か面白い結果を見い出せるかもしれないと思い、遊び感覚で研究を始めました。得られた結果を西脇さんに見せたところ、これは論文化すべきという話になり、雑談から始まって、たった 2 週間で論文化という凄まじいスピードで物事が進んでいきました (研究内容の詳細は、トピックス「重富 尚太さんと西脇 瑞紀さんが、非定常核形成速度の時間発展を簡単に推定できる方法を発見しました。(2023年3月15日)」をご覧ください)。