数学科の 1 年前期では、コアセミナー I という専攻教育科目を受講することになっています。数学科の 1 年生が 4 つのグループに分かれ、各グループを担当する数学科の教員が設定した課題図書を読み進めていきます。松坂助教が担当するクラスでは、「せいすうたん 1」という本を毎週 1 話ずつ進めていき、各話の担当者が勉強してきたことを発表します。1 年生の松比良さんと土田さんはゲーベル数列という数列を取り扱った話が担当で、2 人は「せいすうたん 1」には明記されていなかった未解決問題を自ら設定し、その答えについて予想と考察を発表したそうです。その発表を聴いた松坂助教は「問題設定としては完璧、これは面白いことができる」と感じ、3 人でその問題に取り組むことになりました。松坂助教のサポートにより、2 人の予想が正しかったことが証明され、その成果は論文として The American Mathematical Monthly に掲載されることが決まっています。
「せいすうたん 1」は、日本評論社から出版されている数学セミナーという数学雑誌で連載されていた小林 銅蟲 先生による漫画に、青山学院大学の関 真一朗 助教の解説がついて本になったものです。その第 3 話ではゲーベル数列が取り上げられています。数学の詳細は記事の後半で松坂助教に解説していただきますが、コアセミナー I の講義でこの話の担当になった土田さんと松比良さんは「\(N_k\) の最小値は \(19\) である」と予想し、高校で学んだ数学の知識を駆使してその考察を発表しました。
この発表を聴いた松坂助教は、ものすごく衝撃を受けたそうです。というのも、松坂助教は「せいすうたん 1」の執筆の際に著者の関助教と密接に連絡を取り合っており、原稿を何度も読んでいました。ところが、松坂助教と関助教はこの「最小値の問題」という重要なトピックがゲーベル数列に潜んでいることに気がついていませんでした。そのため、「せいすうたん 1」の解説部分には、この問題は明記されていません。しかし、土田さんは無意識に \(N_k\) の表を眺めて、\(19\) より小さい整数がないことが気になったと話します。まさに、1 年生の思いつきがきっかけとなって生まれた研究成果でした。
ゲーベル数列は 1990 年頃に研究されて以来、長らく忘れ去られていました。そんな数列が、どういうわけか「せいすうたん 1」で取り上げられ、今回新たな結果が発表されたことで、世界中の数学者や数学ファンから注目を浴びています。ゲーベル数列のように忘れ去られた数学の問題は山ほどあると思われますが、「せいすうたん 1」にはそんな問題が多数収録されており、とても異質ですごい本だと松坂助教は話します。もしかしたら他の話にも多くの未解決問題が眠っているかもしれません。
世界中の研究者が日々難しい問題に挑戦している中、こんなところに世界を沸かせる問題があったということに驚きました。来年度も同様の講義を行う予定なので、もしかするとまた新たな定理が見つかるかもしれません。今回、どんな定理が生まれたのか、松坂助教に解説していただきます。
みなさんはオンライン整数列大辞典 (OEIS) というサイトをご存知でしょうか。現在、36 万件を超える整数列の情報が集められたオンラインデータベースであり、整数好きにはたまらないサイトです。
何かを計算していて、例えば \(1, 3, 13, 61, 217, \ldots\) という数列に出会ったとしましょう。この数列のことが気になって夜も眠れないことがあるかもしれません。そんなときは OEIS の出番です。OEIS を開いて、この数列を検索してみると、A357749 というページがヒットします。どうやら、2021 年に Yasuaki Gyoda さんによって研究された対象で、方程式 \((x + y)^2 + (y + z)^2 + (z + x)^2 = 12xyz\) の整数解として現れる数列なのだそうです。
このサイトはもともと、「A Handbook of Integer Sequences」という 1 冊の本でした。1973 年に出版されたこの本は、約 2400 項目からなる数列コレクションでしたが、出版後、多くの数学者から様々な整数列が提供されるようになり、現在の形まで進化を遂げました。その中で生まれたのが、本研究の主題である「ゲーベル数列」です。
1975 年のある日、数学者レンストラから本の著者スローンへ、1 通の手紙が届きます。ゲーベルに教えてもらった数列が面白いのだけれど、整数列かどうか分からないので、コレクションに相応しいかどうかも分からない、というのです。その数列というのがこちら：初項を \(g_0 = 1\) として、\(n\) 番目の項 \(g_n\) を漸化式
で定めます。最初のいくつかを計算してみると、
となり、さらに \(g_4 = 10,\, g_5 = 28,\, g_6 = 154,\, g_7 = 3520\) と続きます。実はこのとき、とても不思議なことが起こっていることに気がつきます。定義によると、\(n\) 番目の項を計算するときに、\(n\) で割る必要があるため、一般に \(g_n\) は分数の形になってしまいそうなものです。にも関わらず、今のところ \(g_n\) はすべて整数です。もっと計算を進めて
まで整数であることも確かめられますが、少なくとも手計算ではこれ以上の計算は厳しそうです。
この「\(g_n\) が整数である」という状況は、未来永劫、いつまでも続くのでしょうか。この問題は、当時界隈を悩ませたようですが、同 1975 年に同じくレンストラによって解決します。いわく、\(g_{42}\) までは整数だけれど、\(g_{43}\) でついに整数でなくなってしまうのだそう。\(g_{43}\) の整数部分は大体 1800 億桁で、Microsoft Word で 1 ページ 1440 桁書いたとしても 1 億ページ以上必要になるような大きな数ですから、計算機を用いたとしても確認するのは大変そうです。
ともかく、残念ながらゲーベルの数列は整数列ではありませんでした。しかし、それはそれで面白いということでしょうか、現在では OEIS の A003504 に収録されています。
ゲーベル数列の漸化式の \(2\) 乗の部分を \(3\) 乗に変えると何が起こるでしょうか。そんな疑問を持った数学者がいました。ここではさらに一般に \(2\) 乗の部分を \(k\) 乗に取り替えた、\(k\)-ゲーベル数列を考えてみましょう。\(2\) 以上の整数 \(k\) に対し、初項を \(g_{k,0} = 1\) として、\(n\) 番目の項 \(g_{k,n}\) を漸化式
で定めます。例えば \(k=3\) のとき、
となり、さらに \(g_{3,4} = 22815,\, g_{3,5} = 2375152056927\) と続きます。\(3\) 乗になったので、先ほどよりも大きくなるのが早いですが、やはりこの場合も不思議と整数が続きます。しかし、この場合も残念ながら、89 番目の項 \(g_{3,89}\) でついに整数でなくなってしまうことが知られています[1]。さっきよりも長いこと整数であり続けられるようです。では、\(k=4\) や \(k=5\) ではどうでしょうか。
2020年、雑誌「数学セミナー」で連載されていた漫画「せいすうたん」において、この問題が紹介されました。\(k\)-ゲーベル数列の整数性が崩れてしまう番目のことを \(N_k\) と書くことにしましょう。例えば、\(N_2 = 43,\, N_3 = 89\) というわけです。このとき、\(k=61\) までの結果が次の表のように計算されています。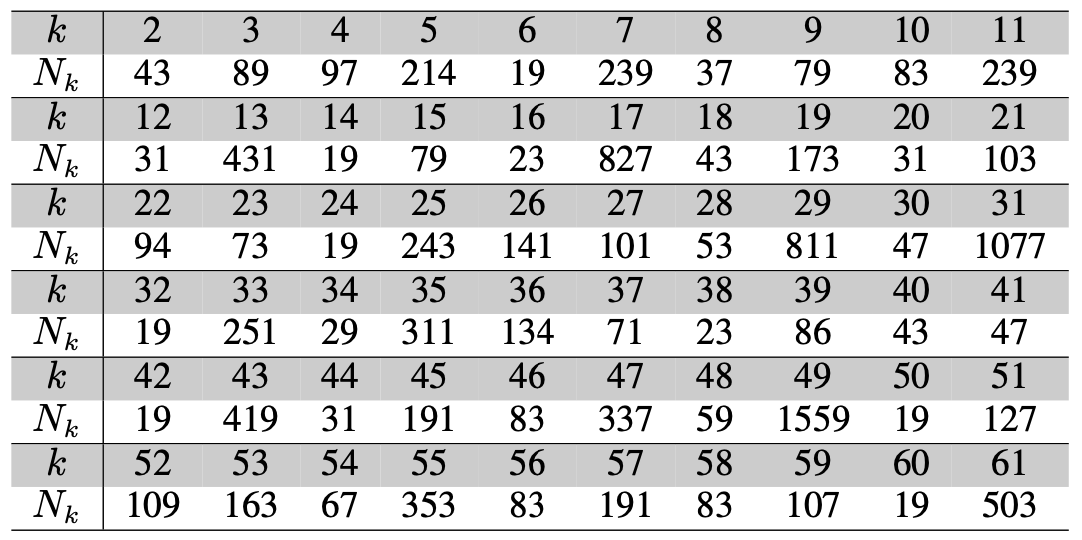
今、我々は新たな数列 \(N_k\) に出会いました。何か面白い発見はできるでしょうか。まずはじっくりと表を観察してみることにしましょう。すると \(N_k\) の値は不規則に揺れ動いていることに気が付きます。例えば、\(k=6\) のときには \(19\) 番目で早々に整数でなくなってしまうようですし、\(k=49\) のときは、なんと \(N_{49} = 1559\) ということで、かなり長いこと整数が続くようです。
土田さんや松比良さんも、この \(N_k\) のリストを独自の視点で観察し、「\(N_k\) の最小値」に関する考察を行いました。実は後で気がついたことなのですが、漫画の中で、あるキャラクターが「\(N_k\) の最小値」が気になるという話をしています。この問題を真剣に考えてみることにしましょう。上の表を見る限りでは、\(N_k\) の最小値は \(19\) のようです。しかしたった \(60\) 個の例を計算しただけで、\(N_k\) の最小値が \(19\) だと断言できるでしょうか。少ない例から数列の正体を見抜くことの難しさは、他でもない、ゲーベル数列から学んだはずです。もしかしたら \(k=100\) くらいまで考えてみると、\(7\) 番目くらいで早々と整数でなくなってしまうような例が見つかるかもしれません。
しかしながら数値実験をしてみようにも、\(k\)-ゲーベル数列はものすごい勢いで大きくなる数列なので、計算機を用いたとしても \(N_k\) を直接調べるのは難しいです。何より最小値というからには、無限個の \(k\) に対して \(N_k\) を知る必要があります。一体、どうやってこの数列を研究すれば良いのでしょうか。
それでは、答え合わせです！次の定理が今回我々が得た結果になります。
「\(19\) が最小値かも」という直感が正しかったことに加え、いつ \(N_k\) が \(19\) と等しくなるかも完全に特定することが出来ました。一体どうやって \(N_k\) の最小値を知ることが出来たのか、鍵となった 3 つのアイデアを簡単に紹介しましょう。
こうして、小規模ながらも「理論と計算機の共同作業」という形で問題を解決することが出来ました。
最後に次に解くべき最も基本的な問題を一つ残すことにしましょう[3]。
松比良さん :
理系や文系に限らず様々な科目が好きでしたが、自分の専門を 1 つ選ぶなら数学かなと思い、数学科に入学しました。
土田さん :
数学ができる方だとは思っていませんが、数学の授業を受けるのが好きで数学科に入学しました。
松坂助教 :
定理の証明には、実は高度な数学はそれほど使っておらず、分かってしまえば高校生でも証明できるかもしれないようなものでした。まさに、コロンブスの卵です。
Note:
より詳しく知りたい方は・・・