九州大学 理学研究院 理学府 理学部

ピタゴラス数とフェルマーの最終定理

　突然ですが、次の簡単な方程式を考えます。

この方程式を満たすような正の整数の組 \((x,y,z)\) には、どのようなものがあるでしょうか？考えるまでもなく、\(1+1=2\) や \(2+3=5\)、\(3+4=7\) など、(当たり前とも思える) 解が無数にあることに気が付くと思います。

　それでは、「正の整数」の代わりに「平方数 “square number” 」の組 \((x,y,z)\) を考えてみると、どうでしょうか？少し難しくなりますが、この場合にも、\(3^2+4^2=5^2\) や 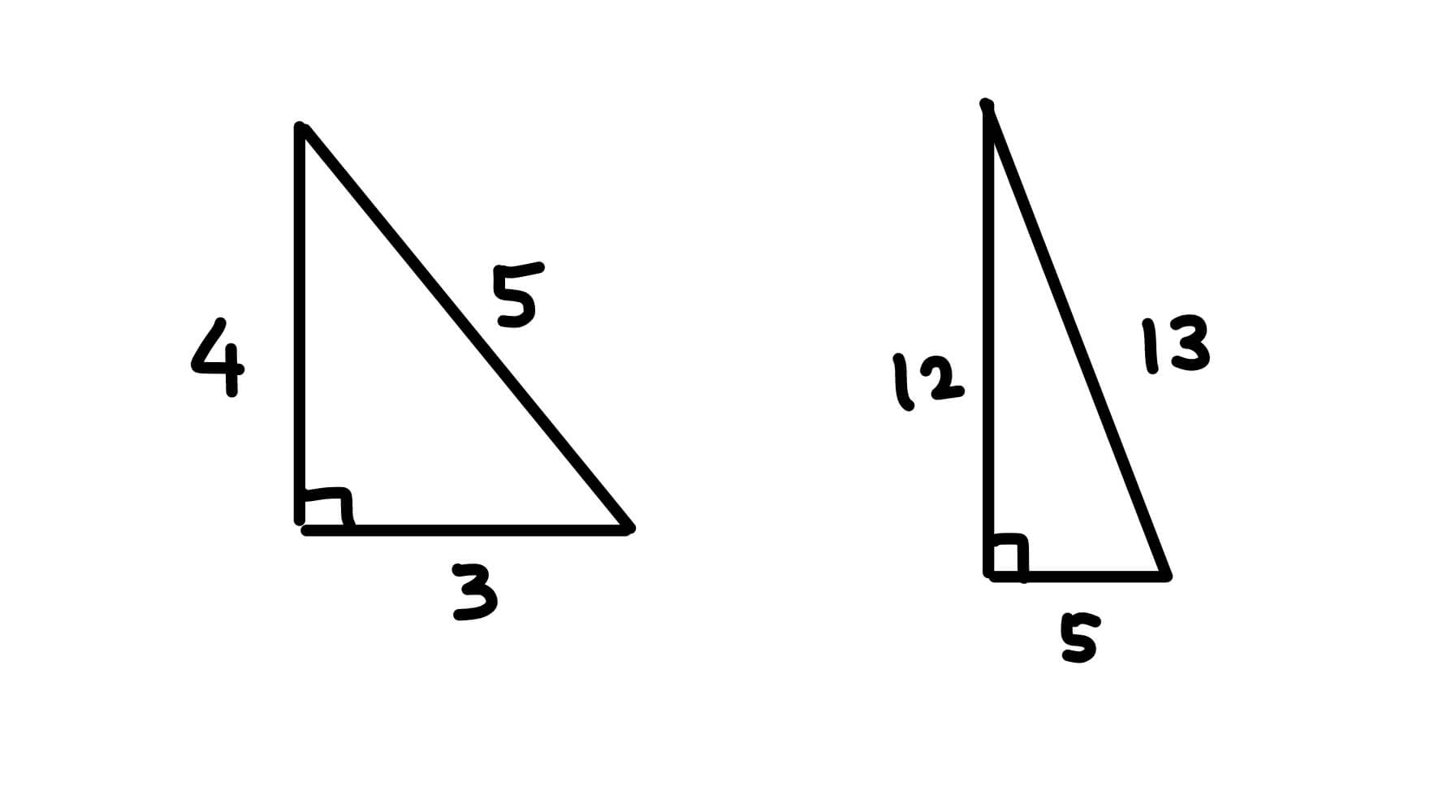\(5^2+12^2=13^2\)、\(8^2+15^2=17^2\) などの幾つかの解があることに気が付きます。実際、\(x^2+y^2=z^2\) を満たす組 \((x,y,z)\) はピタゴラス数 “Pythagorean triple” と呼ばれ (図1)、最大公約数が \(1\) のもののみを考えても^[1]、やはり無数に存在することが古くから知られています。

　では同様に、「平方数」の部分を「立方数」や「\(4\) 乗数」「\(5\) 乗数」などに取り替えても、方程式の解は無数に見つかるでしょうか？ . . . (考え中) . . . いくら考えても \(1\) 組も見つかりません。実は \(3\) 乗以上の場合は「フェルマーの最終定理 “Fermat's Last Theorem” 」として知られる超有名問題で、1995 年にアンドリュー・ワイルズによって\(1\) 組も解が存在しないことが証明されています。

\(2.1\) 乗数？

　ここまでの話は有名なので、数学好きの方であれば、どこかで聞いたことがあったかもしれません。それでは、次のような中途半端な状況を考えるとどうでしょうか？

　まずは「\(2.1\) 乗数」の意味をはっきりしておきましょう。ここでは単に整数を \(2.1\) 乗^[2]したものではなく、その整数部分を取ったものを「\(2.1\) 乗数」と呼ぶことにします。例えば、

なので、「\(2.1\) 乗数」の集合は \(\{1, 4, 10, 18, 29, 43, \ldots\}\) となります。専門用語を用いれば、任意の実数 \(\alpha>0\) に対して定まる集合

は指数 \(\alpha\) の Piatetski–Shapiro 列 “Piatetski–Shapiro sequence with exponent \(\alpha\)” と呼ばれます。上の例だと、\(\mathrm{PS}(2.1) = \{1, 4, 10, 18, 29, 43, \dots\}\)、\(\mathrm{PS}(2) = \{1,4,9,16,25, 36, \dots\}\)というわけです。ここで、\(\lfloor x \rfloor\) は \(x\) の整数部分 “integer part of \(x\)” を表しており、ガウス記号や床関数 “floor function” と呼ばれたりします。

　では早速、問題について考えてみましょう。「\(2.1\) 乗数」をもう少し沢山計算してみると、

と続きます。このリストの中に、\(x+y=z\) が成り立つような組 \((x,y,z)\) はあるでしょうか？ . . . (考え中) . . . 注意深く眺めてみると、\(59+125=184\)、つまり、\(\lfloor 7^{2.1}\rfloor+\lfloor10^{2.1}\rfloor=\lfloor12^{2.1} \rfloor\) が成り立つことに気が付きます。他にも \(43+294=337\) や \(153+184=337\) なども見つかり、「\(2.1\) 乗数」に対して上の問題の答えは「Yes」であることが分かります。さらに Mathematica^[3]を用いて \(\lfloor100^{2.1}\rfloor = 15848\) までの範囲でサーチしてみると、もっと沢山の解が見つかります (図2)。

　大胆なことを言えば、無数の解があるかもしれません。一方で、「\(3.2\) 乗数」を計算してみると、\(2^{3.2}=9.18\)、\(3^{3.2}=33.63\) などの整数部分を集めて、

となりますが、この小さなリストを見ている限りでは、\(x+y=z\) を満たすような組は見つかりません。さらに計算機を用いて探索範囲を広げてみましたが、少し計算しただけでは解 \((x,y,z)\) は見つかりませんでした。

どんな \(\alpha\) なら解があるだろうか？

　この疑問を深掘りしてみましょう。ここまでで分かったことをまとめると、次のようになります。

　この数少ないデータから、どんな \(\alpha\) 乗数なら \(x+y=z\) を満たす組 \((x,y,z)\) が存在するか、予想してみましょう。さらにもう一歩大袈裟に考えて、「解が無限個ある」か、「解が有限個 (0 個も含む) しかない」かの 2 択で場合を分けて考えてみることにします。現状分かっているのは、「\(\alpha=1,2\) のときは解が無限個あり、\(\alpha=2.1\) のときも解が無限個ありそうな気がする、そして \(\alpha=3,4,5,\dots\) のときは無限個どころか 1 つも解はない」ということです (図3)。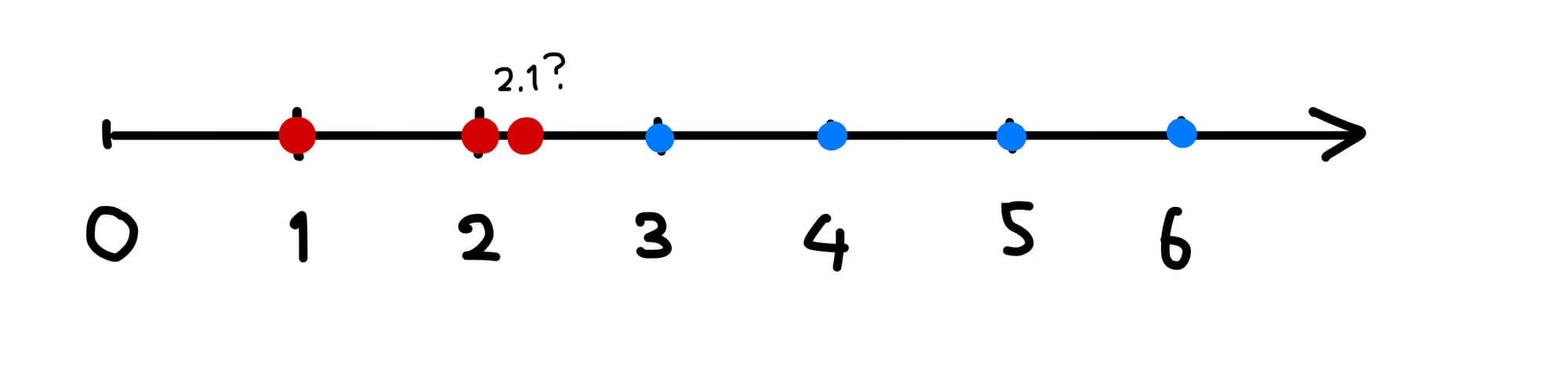

予想 1.　どこかに境界 \(\alpha_0\) が存在して、\(\alpha\) が \(\alpha_0\) より大きいとき解は有限個 (0 個も含む) しかない。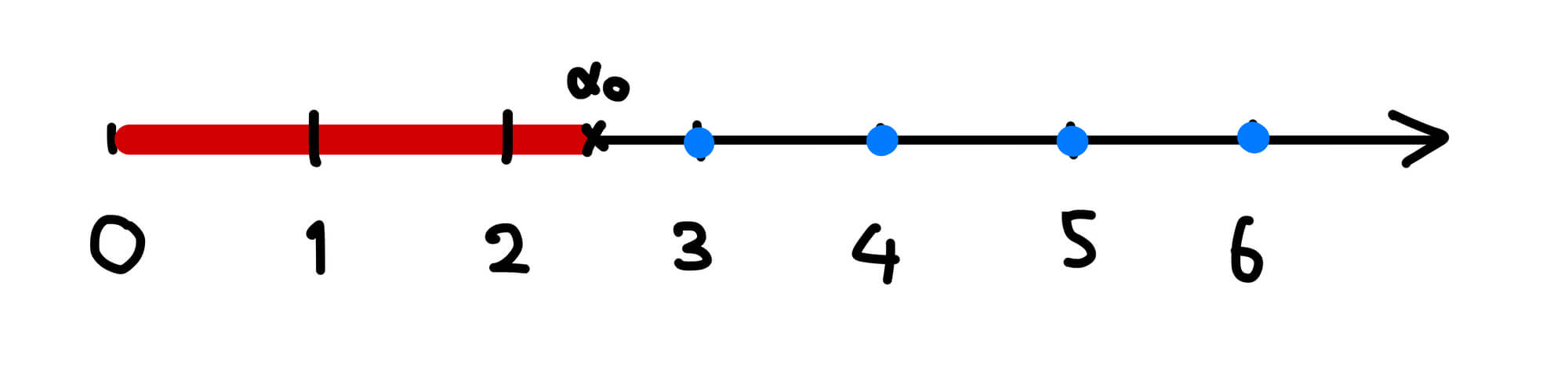

予想 2.　解の有無について明確な境界はなく、\(\alpha\) が大きいときにも無限個解が見つかることがある。しかし、解が無限個あるような大きな \(\alpha\) はかなり稀である。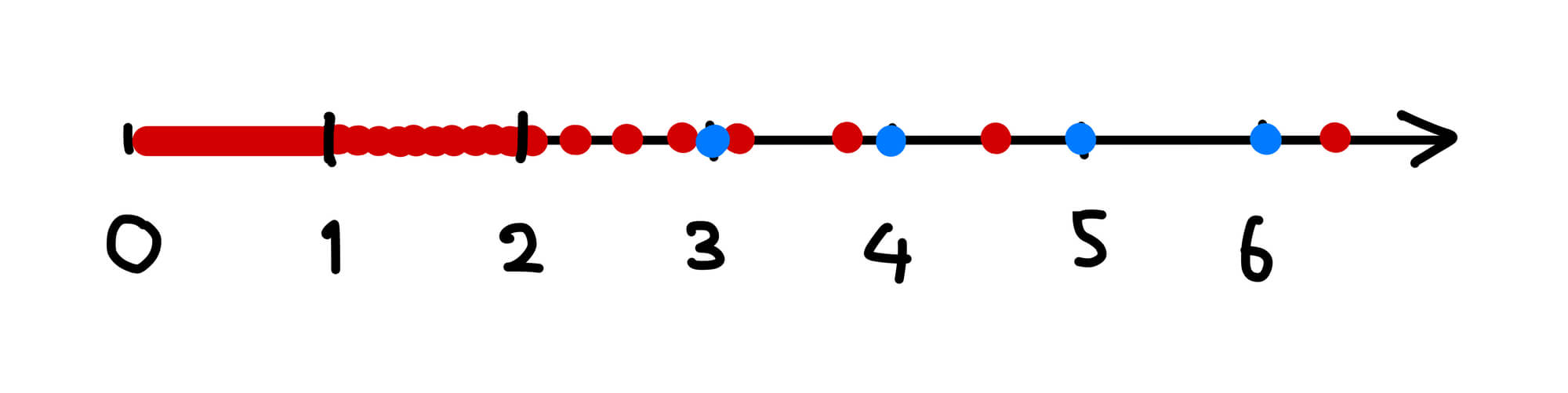

予想 3.　大きな \(\alpha\) であっても、無限個の解を持つような \(\alpha\) は物凄く沢山ある。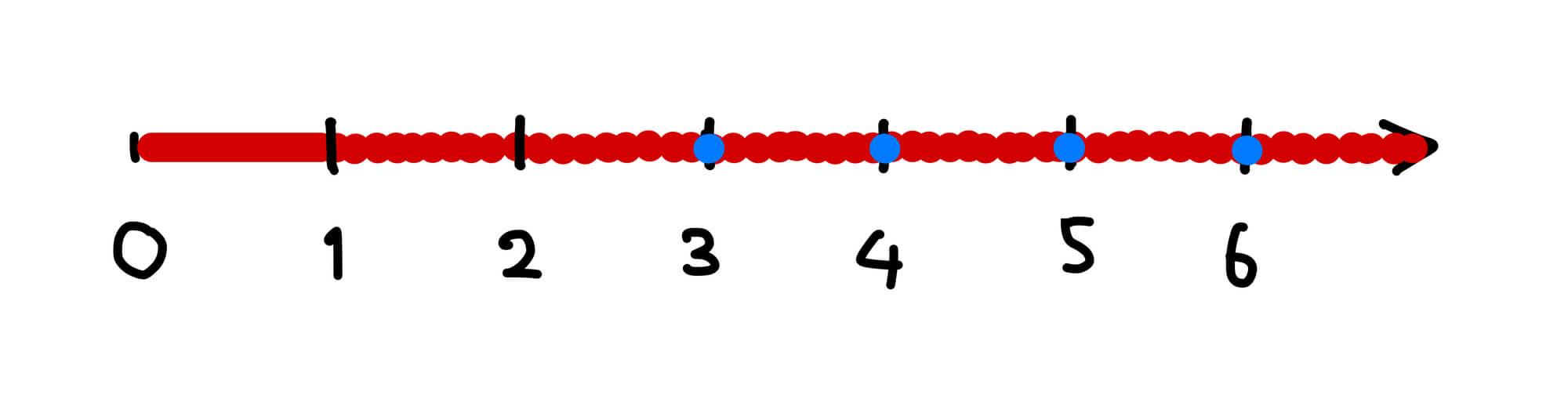

予想 4.　実は \(3\) 以上の整数 \(\alpha = 3, 4, 5, \dots\) のみが例外であり、その他の \(\alpha\) については無限個の解を持つ。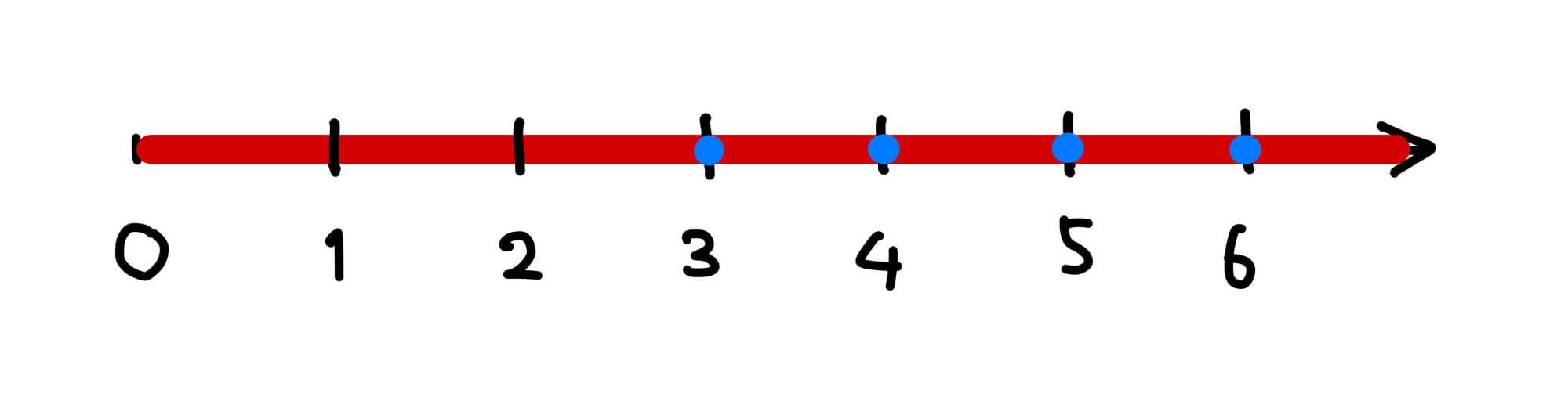

齋藤 耕太 氏との共同研究

　私がこの問題に出会ったのは、2020 年 6 月 26 日の齋藤 耕太くん (図4、現在：筑波大学の学振 PD、当時：名古屋大学の博士 2 年生）の講演を聞いたときでした。彼は「疎な集合の構造をフラクタル幾何学を用いて調べる」ことに長けた国内では唯一無二の専門家であり、この日も Piatetski-Shapiro 列に関する問題について研究発表を行っていました。当時の私はこの手の研究について全くの素人だったのですが、彼の講演を聞いてこの問題に興味を持つようになり、すぐに齋藤くんと一緒に研究を始めることにしました。

　きっかけは、計算機を使って色々な \(\alpha\) 乗数を調べてみたところ (図2)、想像以上に解が沢山見つかるという現象に直面したことです。実は、最初に講演を聞いたときは「問題の答えは予想 1 のような状況か？」という印象を受けたのですが、色々と実験をしていく中で「予想 2 のような状況もありうるかもしれない」と思うようになってきました。

　結論を述べてしまうと、我々の共同研究において明らかになったことは、上の問題の答えは少なくとも予想 3 (！) のような分布になっている、という驚くべき事実でした。数学の言葉で記述すると次のようになります。

　具体的な証明については解析数論やフラクタル幾何学のテクニックを用いるため、ここで詳しく説明することはできませんが、解を沢山見つける仕組みについて物凄く大雑把に説明すると、まず実数の連続性 (中間値の定理) を用いることで、

を満たすような正の整数の組 \((x,y,z)\) と実数 \(\alpha>0\) を沢山見つけます。ここで単に各項の整数部分を取ってみても、\(\lfloor x^\alpha\rfloor+\lfloor y^\alpha\rfloor=\lfloor z^\alpha \rfloor\) は一般に成立しないのですが (「整数部分を取る」という操作は、簡単そうで意外と難しい)、実は両辺を適当に \(n^\alpha\) 倍してから整数部分を取ると、等号が保たれることが分かります。つまり、

が成り立つような正の整数 \(n\in\mathbb{N}\) が存在するのです。

　こうして、\(x+y=z\) が \(\alpha\) 乗数の解を持つような実数 \(\alpha\) を沢山見つけることができます。さらに我々の研究では、この \(\alpha\) たちが一般カントール集合 “Cantor set” (図5) という一種のフラクタル構造 “fractal structure” ^[5]を備えていることを発見しました。

　この一般カントール集合のハウスドルフ次元 “Hausdorff dimension” ^[6]を評価することによって、より定量的な \(\alpha\) の分布が分かり、その帰結として、上で述べた我々の定理を得るのです。

まとめと展望

　今回の研究は、フェルマーの最終定理という超有名問題を題材にして、「\(2.1\) 乗数のような中途半端な状況を考えたらどうなるか？」というある種の素人的発想から始まりました。そして、「\(x+y=z\) を満たす \(\alpha\) 乗数の組 \((x,y,z)\in\mathrm{PS}(\alpha)^3\) が無限個存在する」ような \(\alpha\) が極めて沢山ある、という面白い事実を突き止めることに成功したのです。

　しかしながら、まだまだ分からないことも沢山あります。例えば、問題の答えが予想 4 のような状況になっているか否かは、未だ分かっていません。もっと言えば、先ほど \(\alpha=2.1\) のときは無限個解があるかも、と主張しましたが、本当に無限個の解があるか証明はできていませんし、\(\alpha=3.2\) の場合も探してみた範囲には解がなかっただけで、本当に 1 つも解がないのか、はたまた頑張って探せば解がたくさん見つかるのか、ということも難しい問題のままです。

　実はこの共同研究、最初のモチベーションは別のところにあり、「\(\alpha\) 乗数からなる等差数列を探す」ことが本来の目的でした。等差数列 “arithmetic progression” とは、おそらく高校生の頃に勉強したであろう対象で、例えば \(2.1\) 乗数であれば、

から得られる数列 \(\{4, 218, 432\}\) は長さ \(3\)，公差 \(214\) の等差数列を成します。

　似たような問題に「素数からなる等差数列が存在するか」という問題があります。例えば、\(\{3,5,7\}\) は全て素数で、公差 \(2\) の等差数列ですし、\(\{5,11,17,23,29\}\) は素数からなる長さ \(5\)、公差 \(6\) の等差数列です。もっと長い等差数列が存在するかというと、現状発見されている最大の長さは \(27\) のようですが、実は一般に「素数からなる任意の長さの等差数列が (具体的には分からないが) 存在する」ことが、グリーンとタオによって 2008 年に証明されています。

　この「ある集合の中に等差数列がどれほどあるか？」という問題は、「等差数列」という単語から受ける初等的な印象とは裏腹に、長い歴史を持つ王道とも言える研究領域の一つです。今回の共同研究では、\(\alpha\) 乗数からなる長さ \(3\) の等差数列を沢山見出すことにも成功していますが、残念ながら \(\alpha\) 乗数からなる長さ \(4\) や長さ \(5\) の等差数列がどれほど存在するのか、現状全く分かっていません。はてさて、今後どのような現象が我々を待ち受けているのでしょうか、乞うご期待です。