

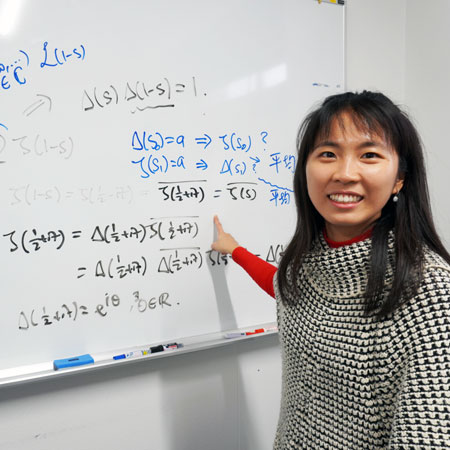
「素数」と聞くと、わたしたちの生活とかけ離れたもののように思われるかもしれません。しかし、実は情報社会が成り立つためには素数が無くてはならない存在であり、通信の安全性は素数によって保たれているのです。
本稿では、そんな素数が魅せる不思議な世界について数理学研究院のアデ イルマ スリアジャヤ先生に解説していただきます。素数とは何なのか? どれくらいたくさんあるのか? という素朴な疑問からはじめて、「素数の分布」と数学界の未解決問題「リーマン予想」のつながりや先生ご自身の研究に至るまで、ワクワクするような数学の物語へと飛び込んでみましょう。

パソコンやスマートフォンなどの電子機器は、私たちの生活に欠かせない存在です。新しい電子機器が次々と開発され、これほどに普及してきたのは、「暗号化」という技術が発展してきたからです。個人情報が他人に漏れないか、友達とのやりとりが第三者に伝わらないかが気になりますよね。このような電子情報を守るための技術は「暗号理論」によって実現されます。暗号理論を開発する初期段階では、素数の性質が必要不可欠なものとなっています。まずは素数と暗号理論との関係について少しだけ触れて、素数自身の面白さについて語りたいと思います。
さて、素数? とは何だっけというみなさん、もう一度思い出してみましょう。一度は耳にしたことがあるかもしれませんが、素数とは、
です。具体的に考えてみましょう。まずは、よく混乱されているので、注意しておきたいですが、1 は素数ではありません。6 は 2 × 3 で書けるので、素数ではありません。このようにして素数を探してみると...
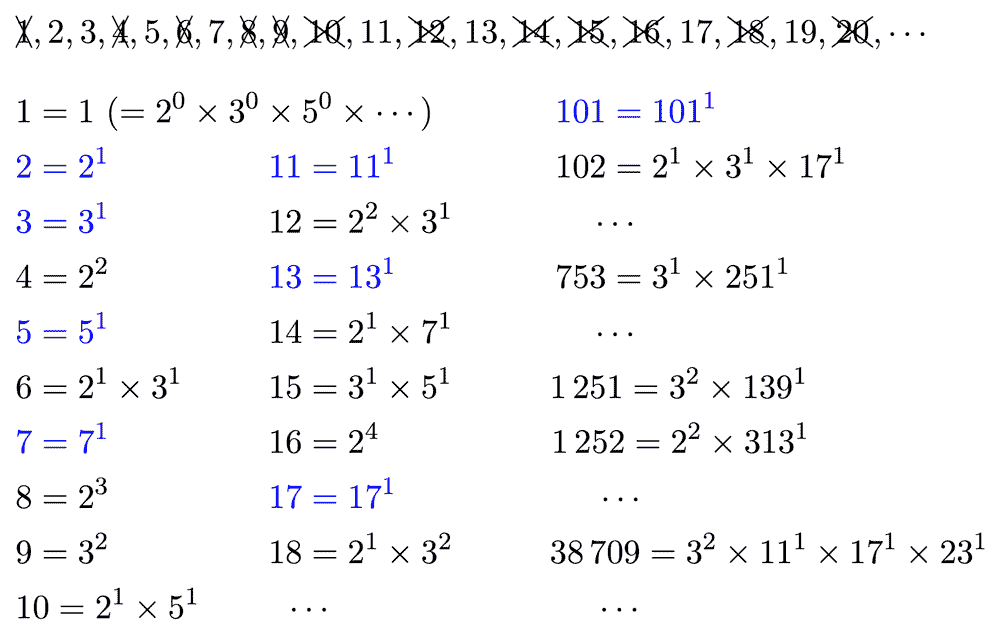
のように次々と素数を見つけることができます。素数を並べてみると、
という素数の列が得られます。すでにお気づきかもしれませんが、素数というものは、あらゆる自然数の「素」となるものです。どんな自然数でも素数のかけ算で表せて、その表し方は一通りしかありません。先ほどの例「6 = 2 × 3」でいうと、自然数「6」はふたつの素数「2 と 3」(素因数) によって分解されています。数学の言葉で言い換えれば、
となります。素数は、自然数を特徴づける大事なパーツなのです。もっと視野を広げて、「負の整数 (−1, −2, −3, −4,... )」や「ゼロ(0)」を入れた整数全体を考えてみましょう。これらは自然数だけから作ることができます。たし算や引き算という演算を自然数に与えればよいのです。自然数は素数に分解できることを思い出すと、結局、整数全体を知るには素数を理解すれば十分なのです。もっといろいろな演算 (かけ算や割り算など) を考えたらどうでしょうか。数学的に厳密な説明を省きますが、実はこのような一般的な数体も整数から構成できます (図3)。
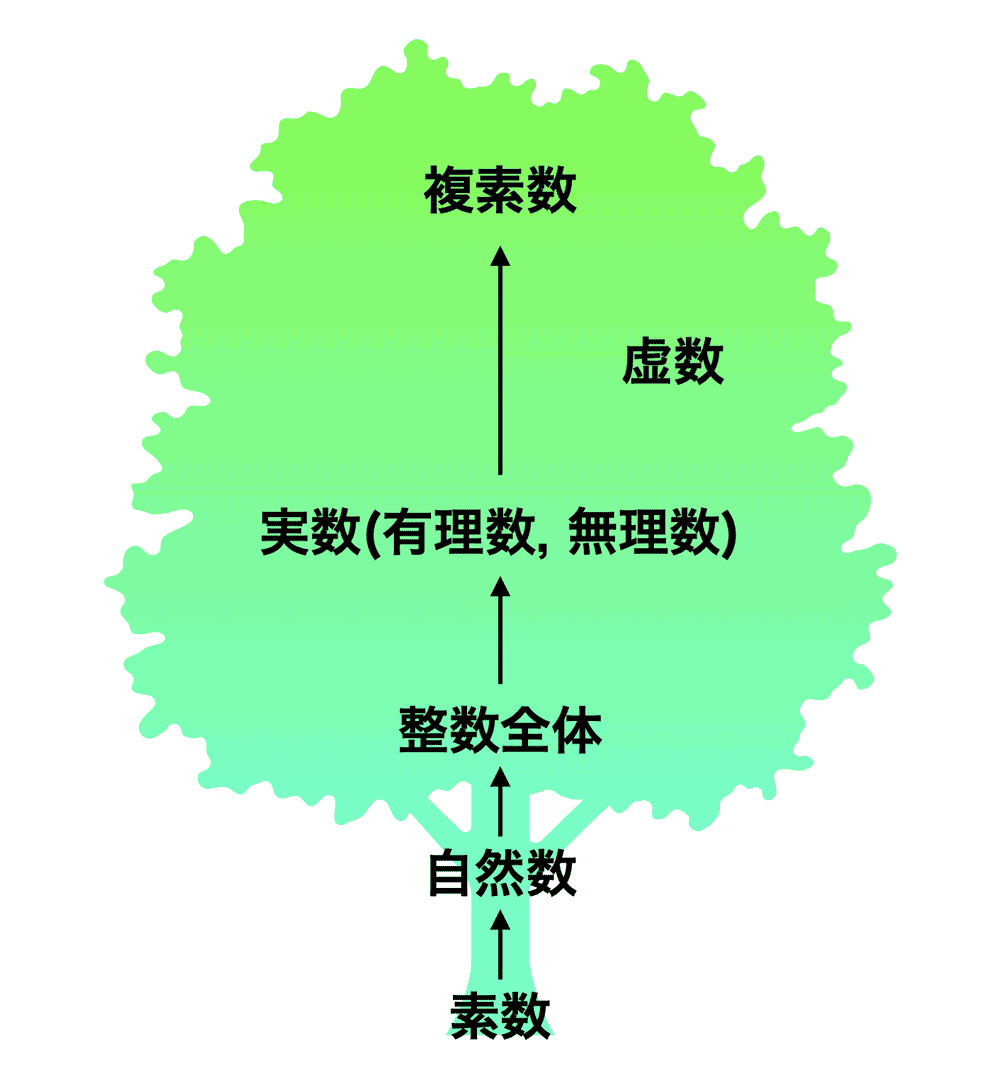
つまり、素数はあらゆる数体の最小単位といえます。物理学における「素粒子」をイメージするとわかりやすいかもしれません。これ以上分解できない最小のモノは素粒子と呼ばれますが、素数は数の世界における「素粒子」のような存在なのです。
素数が暗号に役立つと何となく想像がつきますよね。素数をいくつか勝手に取ってきて、それらを掛けたらどんな自然数になりますか? と聞かれればすぐに答えられるでしょう。しかし、逆に自然数が与えられたとき、その数は素数でしょうか? 素数でなければ、素因数は何でしょうか? と聞かれると簡単には答えられません。具体例で考えてみましょう。
というかけ算 (A) の答えは何でしょうか。筆算すると「10,138,511,081」となることがすぐに分かります。逆に、
は素数でしょうか? 素数でなければ、素因数分解はどうなりますか? という問題は...すぐに答えられないですね。答えを先に言います: (B) 982,451,653 は素数ですが、(C) 1,432,111,263 は素数ではありません。(C) を素因数分解してみると、
となります。手で計算してみれば分かりますが、(B) が素数かどうかの判定や (C) の素因数分解にくらべて、かけ算 (A) はとても簡単です。素因数分解の難しさがお分かりいただけたと思いますが、実はこの概念がそのまま暗号理論に応用されているのです。さきほどの整数 (C) を暗号文だと思いましょう。対応する鍵は、素因数「3, 11, 17, 19, 29, 41, 113」です。鍵を持っている人だけには暗号をすぐに解く (素因数分解する) ことができるのですが、そうでない人は解くのにたいへん長い時間がかかります。
もちろん、(B) や (C) くらいの数であれば、頑張れば手でも計算できますし、パソコンを回せば一秒もかからずに解けます。大事な個人情報を守る暗号としてはまだ頼りないですね。その通りです!暗号の世界では何桁にもわたる巨大な整数が使われており、膨大な素数が必要になります。そこで、素因数分解をするのに、スーパーコンピューターでも何百、何千年の時間が掛かることを利用していて、暗号の安全さは保証されます。まだまだ脆そうで不安に思われるかもしれませんが、ご安心ください。ここでお話ししたのは、あくまでも素数の暗号への応用についてのおおざっぱな解説です。コンピュータの改良とともに暗号の技術も日進月歩していて、より高度で複雑な技術が使われています。ここまでお分かりいただけたでしょうか。
暗号理論において必要なのは、「膨大な素数」かつ「安全な素数」です。でも、素数は簡単に見つかるものではありません。さらに、与えられた巨大な整数が素数かどうかを判定するのも大変です。そこで数学者、とくに数論学者たちは「素数の近似」を考えています。この辺に素数は必ず存在する、かつ、たくさんは存在しないということが分かれば、あとは、必要な素数をその区間で探し出せばいいわけです。
まずは素数の現れ方をイメージするために、素数階段 (図4) というものを考えてみましょう。自然数 x を 1 から順に増やしていって、素数が現れたら階段を一段増やします。たとえば最初の一段目は 2 のときに増えます。さらに大きな x を考えて、3, 5, 7,... と階段を増やしていくと、素数の現れるパターンが見えてきます。x が大きくなるほど、平らなところが増えていくことに気が付きます。他にはどんな特徴があるのでしょうか?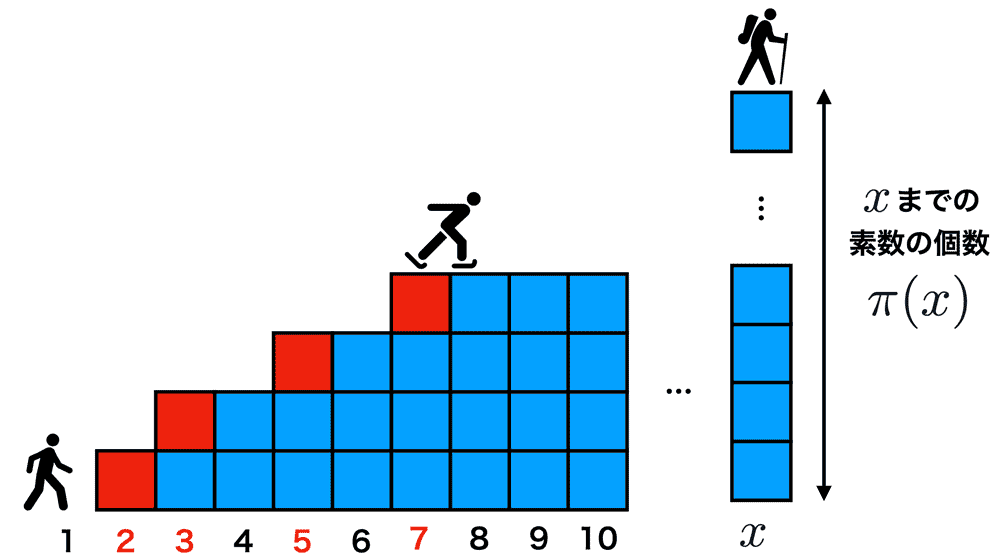
ドイツの天才数学者ガウスは、素数階段がとてもシンプルな式で近似できると予想しました。この予想は後にほかの数学者によって証明され、今日では素数定理として確立しています。素数定理とは、素数の数をかぞえる関数 π(x) (階段の高さ) が
のように近似できるというものです。これを素数階段と比べてみると、その概形を捉えていることがよく分かります (図5) 。
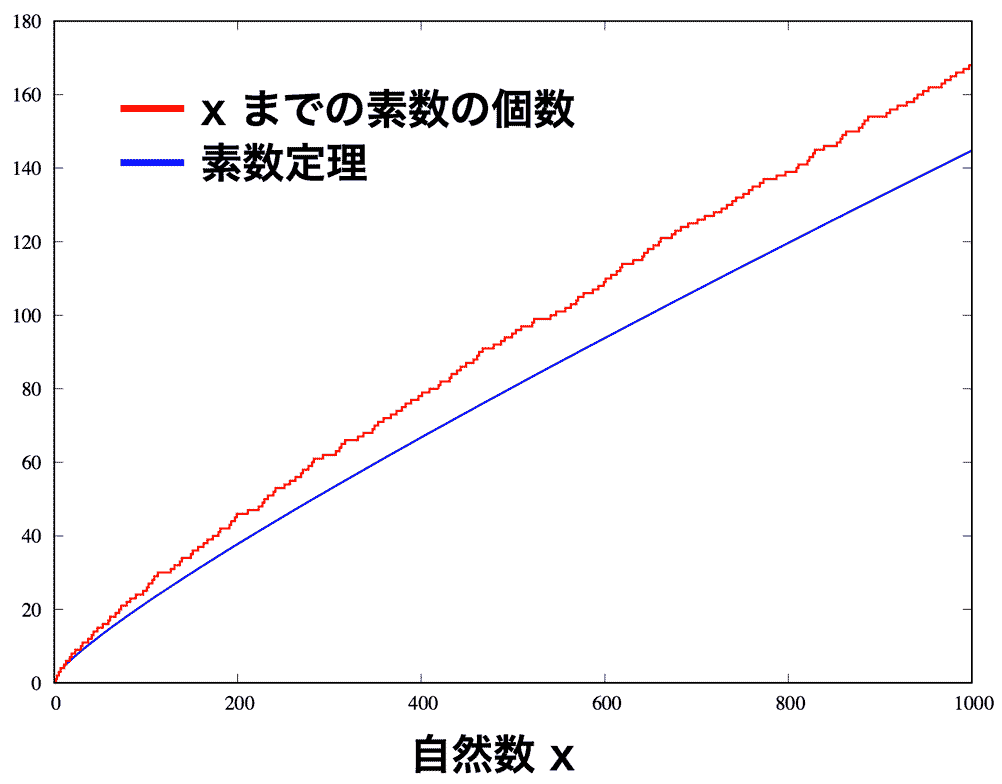
とはいっても、青線がどんどん赤線から離れていきますね。素数定理はあくまで近似公式なので誤差があるのです。この誤差を式で表して、E(x) と書いておきましょう (図6)。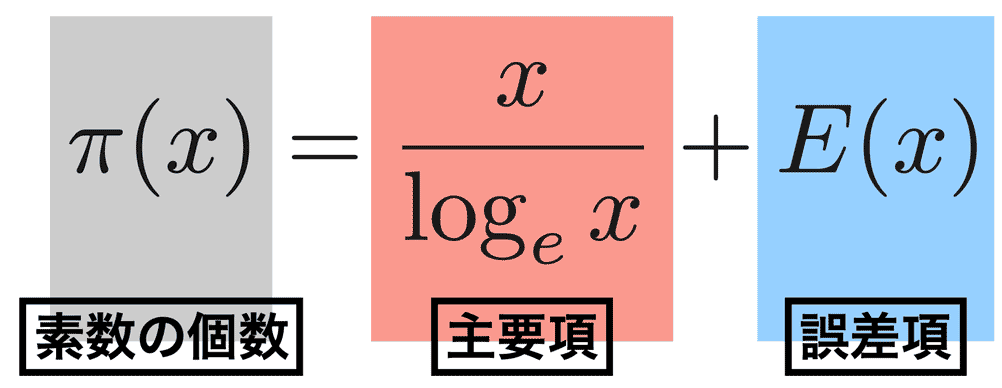
誤差 E(x) には、素数の情報がつまっています。そして、この「誤差 E(x) が増えるスピード」とリーマン予想が深く関わっているのです。もしリーマン予想が正しければ、E(x) の増えるスピードが √x loge x 程度だと証明できます (図7, 赤線)。逆に、もし E(x) が √x loge x のスピードで増えると証明できれば、リーマン予想が正しいといえます。つまり、「リーマン予想を示すこと」と「誤差項のスピードを求めること」は表裏一体の問題なのです。仮に誤差項が √x loge x よりも速く増えると証明できてしまったら...「リーマン予想」は正しくないと示せてしまいます!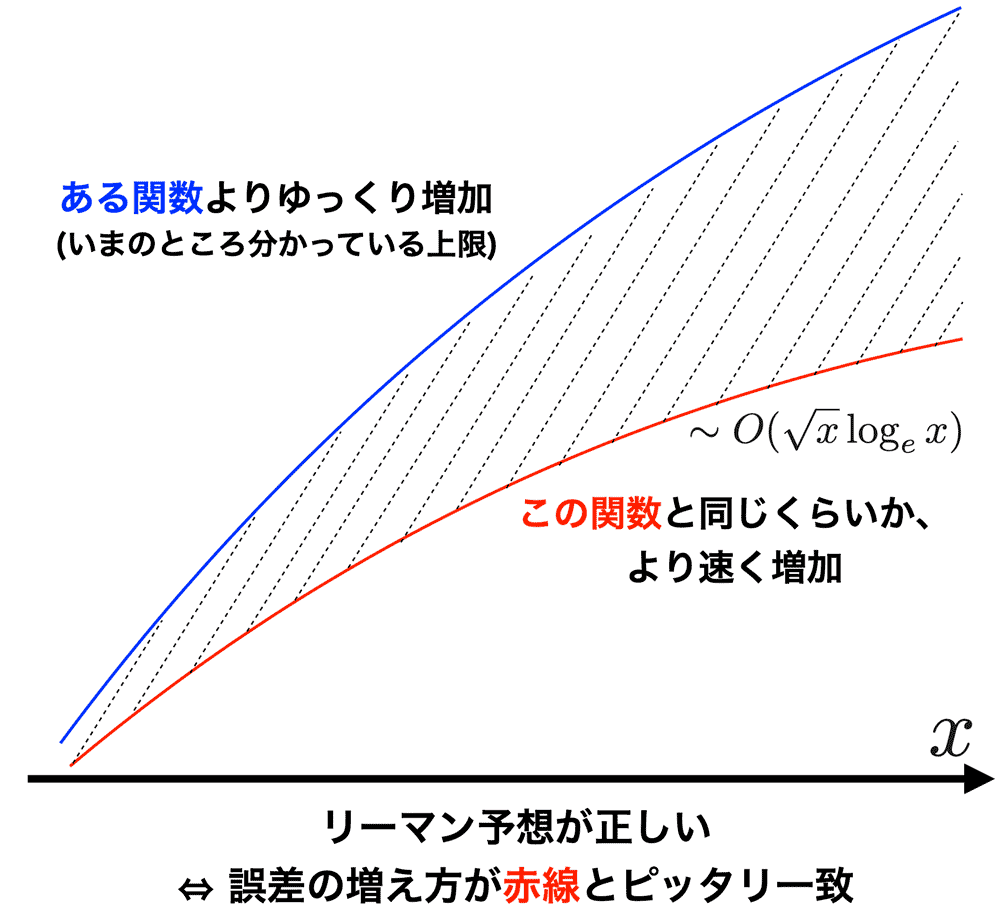
誤差についてどれほど分かっているのでしょうか? 実は、これ以上は改良できないという「下限」がすでに証明されています (図7, 赤線)。さらに突き詰めて、誤差の増加スピードを完全に決めようという試みがなされてきましたが、証明できたのは「ある関数 (図7, 青線) よりは誤差がゆっくり増える」ということだけであり、「下限」からはほど遠く、誤差の完全決定には至っていないという現状があります。
誤差をどうやって見積もるのかという話に移っていきます。実は、誤差を見積もる公式はすでに確立しています。リーマンの素数公式と呼ばれるもので、ドイツ人数学者リーマンによって 150 年以上も前に提案されました。リーマンの素数公式によると、ゼータ関数の性質を調べれば、E(x) を完全に決定できることが示せます。ゼータ関数は何十種類もありますが[1]、リーマンの素数公式に出てくるのは、もっとも基本的なものであるリーマンゼータ関数 ζ(s) です。まずは ζ(s) の紹介から始めたいと思います (図8)。
一般に s は複素数ですが、ここでは簡単のために s が実数の場合を考えてみましょう。
なんだか難しそうな関数 ζ(s) ですが、s が 1 より大きい実数ならば、とてもシンプルな和に化けます: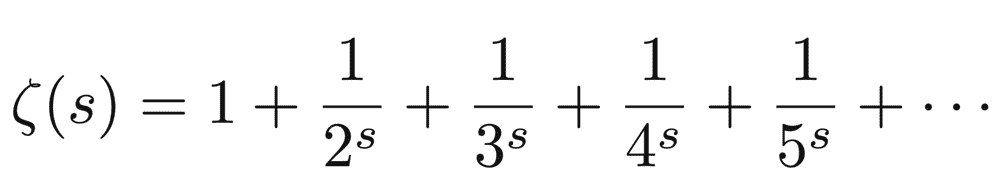
なんとなく自然数、ひいては素数と関係しそうに見えます。たとえば s = 1 のときは ζ(s) が「無限大 (∞)」となりますが (図10)、これは「素数が無限個ある」ということと関係しています。s をもっと大きくしたらどうでしょうか。それぞれの値が小さくなるので有限になりそうですが...たとえば二乗 (s = 2) や三乗 (s = 3) とかを考えると、無限大に行かず、意味のある「数」と等しくなります。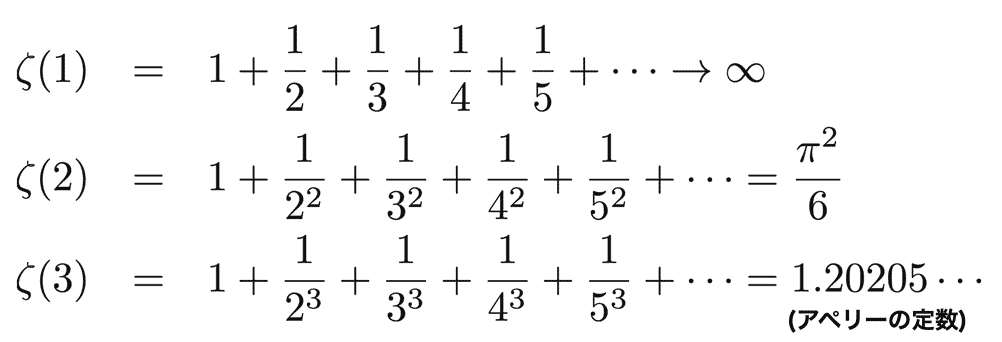
リーマンゼータ関数とは、いろんな種類の「自然数のべき乗和」を内包した関数なのです。
ここから話がぐっと難しくなっていきます。今までは s を実数として s > 1 に限って話してきましたが、これからは s を複素数にまで広げてみましょう。実は s = 1 以外のすべての複素数に対しても ζ(s) はある値をもち、とても性質の良い関数となっています。
とくに面白いのは、ζ(ρ) = 0 になる ρ という点 (零点) です。零点は、自明な零点 (すぐにわかるもの) と非自明な零点 (探しにくいもの) に分類できます (図11)。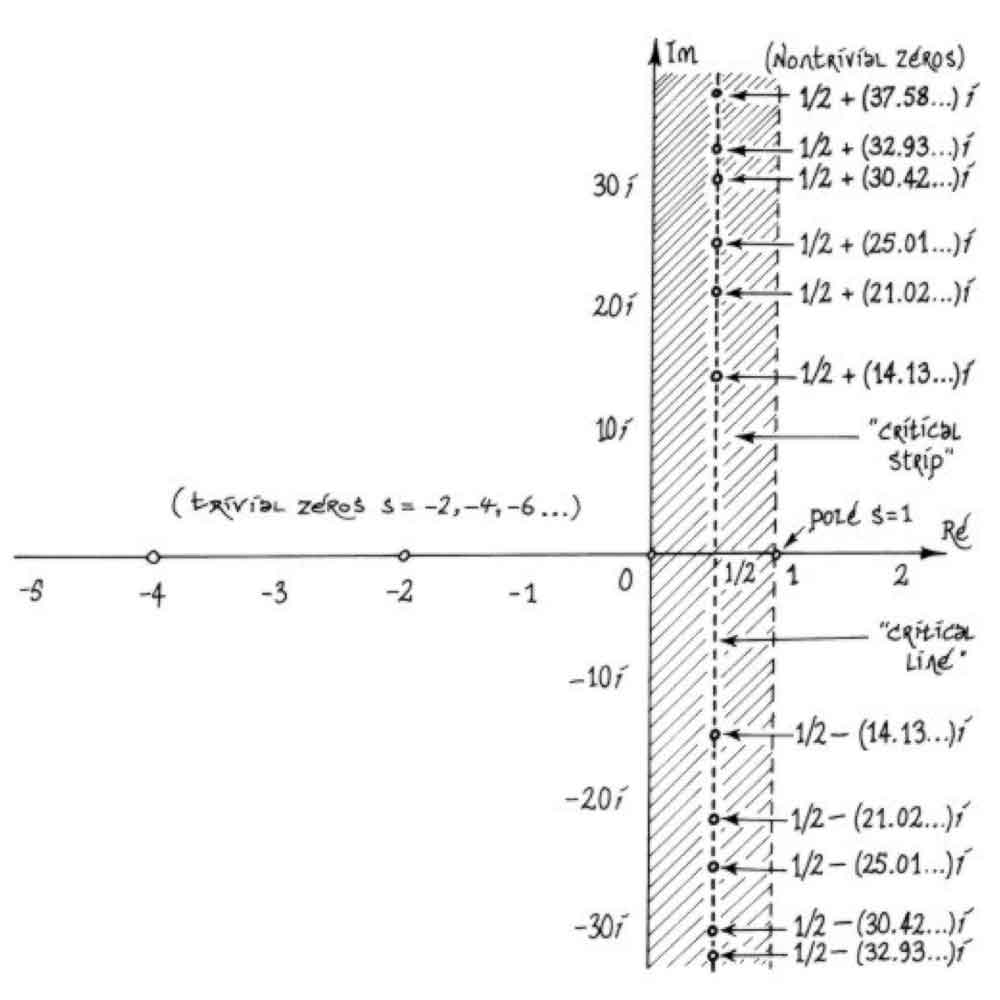

負の実軸上には、零点がポツポツと並んでいます。これが自明な零点です。一方、s の実部が正の領域には、零点が縦に並んでいるのが見えます。こちらが非自明な零点と呼ばれるものです。リーマンの素数公式で誤差を計算するときに、この非自明な零点をインプットする必要があります。つまり「ζ(s) の零点の分布」と「素数の分布」は密接に関係しているのです[2]。こうして ζ(s) は素数の分布を研究するための重要な道具となりました。
リーマン予想とは、
という予想です。たしかに 図11 を見る限りは、実部が1/2となるような一直線上に並んでいますが、これが延々と続く保証はありません。数学的な証明が待たれていますが、150 年以上経った今でも解決されていない難問です。
私は以上で述べたことに動機付けられて、リーマンゼータ関数の零点分布に興味を持っています。長く研究されてきた課題なので、難しい問題ばかり残っていますが、私はなるべく実際の問題から遠く離れないように研究しております。
リーマンゼータ関数 ζ(s) は解析的に良い性質を持ち、ζ(s) を微分した関数 (導関数) を考えることができます。ζ(s) の「一階導関数の零点分布」には、リーマン予想と同値な条件があることは既に知られていました。その後、「ζ(s) の導関数の零点」が「ζ(s) 自身の零点」と関係していることも分かってきました。私はこのような導関数の性質に注目しています。ζ(s) やそれに類似する関数について導関数の零点分布を調べていて、その課題は私が数学者として解いた最初の問題でして、今までも最も興味を持っている問題です。
ここで考えている ζ(s) に類似する関数というのは、特に、リーマン予想が成り立つと予想されている関数たちです。これらの関数族は ζ(s) と同じような特徴を持っていることから興味深い研究対象だといえます。さらに私は、零点だけではなく、値全般 (ζ(s) =「0 以外の定数」) の分布も調べています。
ゼータ関数たちの性質を素数の分布に焼き直すことは、簡単ではありません。頑張って研究してきたゼータ関数たちの性質と素数の分布との対応を見るためには、数論的関数の力を借りる必要があります。そこで私はこの直近二年弱、数論的関数にまつわる問題にも取り組み始めました。
素数は暗号理論に欠かせない存在であり、わたしたちの情報社会は素数によって守られています。素数にはいまだ尽きぬ謎があり、多くの数学者たちを虜にしています。とりわけ「リーマン予想」と「素数の分布」の関係は 150 年以上にわたり調べられてきた難問です。
素数の情報はゼータ関数に密かに隠れています。私はそんなゼータ関数の神秘さと美しさに魅了され研究を進めています。まだ誰も見たことがないようなゼータ関数の一面を少しずつ解き明かすことを目指しています。また、「ゼータ関数のふるまい」と「素数の分布」のより深い関係を探っている途中です。
 私は数学を遅く始めまして、「やはり数学をやりたい」と決心したときに偶然にゼータ関数に出会えて、そもそも好き嫌いの激しい人ですが、その一発で、「この分野をやりたい」「ゼータ関数をやりたい」とすぐに決めました。
私は数学を遅く始めまして、「やはり数学をやりたい」と決心したときに偶然にゼータ関数に出会えて、そもそも好き嫌いの激しい人ですが、その一発で、「この分野をやりたい」「ゼータ関数をやりたい」とすぐに決めました。 そのあと、やはり、誰にでもある不安ですが、この分野は本当に自分に相応しいか、自分が本当にこれでいいのかを心配はしたことがあります。しかし、この分野に潜り込んでやればやるほど好きになる一方です。今の私はただ単にゼータ関数が好きで、知れる限り知りたいという気持ちで研究を続けております。
そのあと、やはり、誰にでもある不安ですが、この分野は本当に自分に相応しいか、自分が本当にこれでいいのかを心配はしたことがあります。しかし、この分野に潜り込んでやればやるほど好きになる一方です。今の私はただ単にゼータ関数が好きで、知れる限り知りたいという気持ちで研究を続けております。
Note:
より詳しく知りたい方は・・・