Web サイトが魅力的なものかどうかを示す指標として「アクセス数」や「平均滞在時間」などがあります。SNS においては「いいね」の数が多いほど、多くの人々の目に留まったことを示しているでしょう。仮に「アクセス数」が少ないとしても、特定の人々に対しては非常に魅力的な Web サイトである場合もあります。数理学府 数理学専攻 藤澤研究室の吉田さんらは、ヤフー株式会社との共同研究で、ネットサーフィンをするユーザーの動きをグラフ理論・数理最適化・統計学を用いて解析し、Web サイトの新たな魅力度を表す指標を提案しました。本指標により、各ユーザーに価値のあるコンテンツ (つまり「おすすめ」) の提供が、より効果的に行えるようになると考えられます。この研究成果は、Data Science and Engineering に掲載されています。
また、Web サイトの解析に限らず、吉田さんらは、実社会の様々な問題の解決に数理最適化などの数学を用いて取り組んでいます。その一例として、自転車シェアリングサービスの自転車再配置最適化の研究を後半で紹介します。これらの技術は、超スマート社会 (Society 5.0) の実現に向けたコア技術として注目されています。
この文章を読まれているあなたは、どのようにしてこの Web ページに辿り着いたのでしょうか？ 九州大学へ進学したい高校生かもしれませんし、九州大学の学生さんかもしれません。たまたま検索に引っかかって、辿り着いた方もたくさんいらっしゃるでしょう。このようにWeb サイトには様々な属性の人々が訪れます。さらに、訪問者の興味も多種多様です。「九州大学ではどのような研究が行われているか？」について知りたい人もいれば、「数理最適化」などの専門用語に惹かれてクリックした人もいるはずです。一方で、個人や企業の Web サイトへの訪問者を増やしたい人が、「アクセス解析」の文字を見て、この Web ページを訪れることもあるでしょう。このように、多くの特性を持った人々が Web サイトを訪れる状況の中で、各ユーザーの興味を機械的な方法で、適切に判断するのは容易ではありません。
ネットサーフィンをするユーザーに、興味を持ちそうな Web サイトや商品を見つけて提案することは Web マーケティングにおいて重要な問題です。ただし、各ユーザーの興味は様々なので、次に訪れる価値のある「おすすめ」な Web サイトやコンテンツを提案するためには、単なる「アクセス数」などの指標を用いることは効果的であるとは限りません。このような指標は、算出が簡単というメリットはありますが、各個人の興味という詳細な情報はかき消されてしまっています。それでは、これまで見ていた Web サイトの履歴や各 Web サイトの閲覧時間から、その人の興味を推測するのはどうでしょうか？この方法は、「アクセス数」よりも効果的な「おすすめ」を提供することが期待できます。そのためには、履歴や閲覧時間などのデータからどのように本質的な情報を取り出し、指標として数値化するかを考えなければなりません。
吉田さんらは今回の研究で、ユーザーのアクセス履歴から得られる下記 2 つのデータを用いました。
まずはユーザーの興味を推測するために、(1) のデータを (図2) の一番左のように、行にユーザー、列に Web サイトを並べて、表で整理してみましょう。表の各要素には、各ユーザーが各 Web サイトを閲覧した時間が記入されています。このデータが並んだ表を、別の 2 種類のデータが並んだ 2 つの表に分割します。この分割方法には、理系の大学 1 年生の全員が勉強する線形代数が応用されています[1]。分割された表の一方 (図2の真ん中) は、行ごとに各ユーザーがどのような興味・関心を持っているかを表しています。具体的には、列にどのようなジャンルの興味を持った集団 (グループ)[2]かの項目を並べ、各ユーザーがどのグループに所属しているかを表します。例えば、(a) 科学に興味がある、(b) スポーツに興味がある、(c) 音楽に興味がある、という 3 つのグループがあるとします。A さんは、科学にはとても興味があり、スポーツと音楽にも少し興味があるとすれば、A さんの行には、表の分割の結果(0.6, 0.2, 0.2)のような数値が入ると想定されます[3]。もう一つの表 (図2の一番右) では、行に興味関心のグループ、列に Web サイトを並べ、どのような興味を持った人がその Web サイトに訪れやすいかを表します。このような分割が可能であれば、膨大な閲覧データからユーザーの興味に関する情報を取り出すことができます[4]。
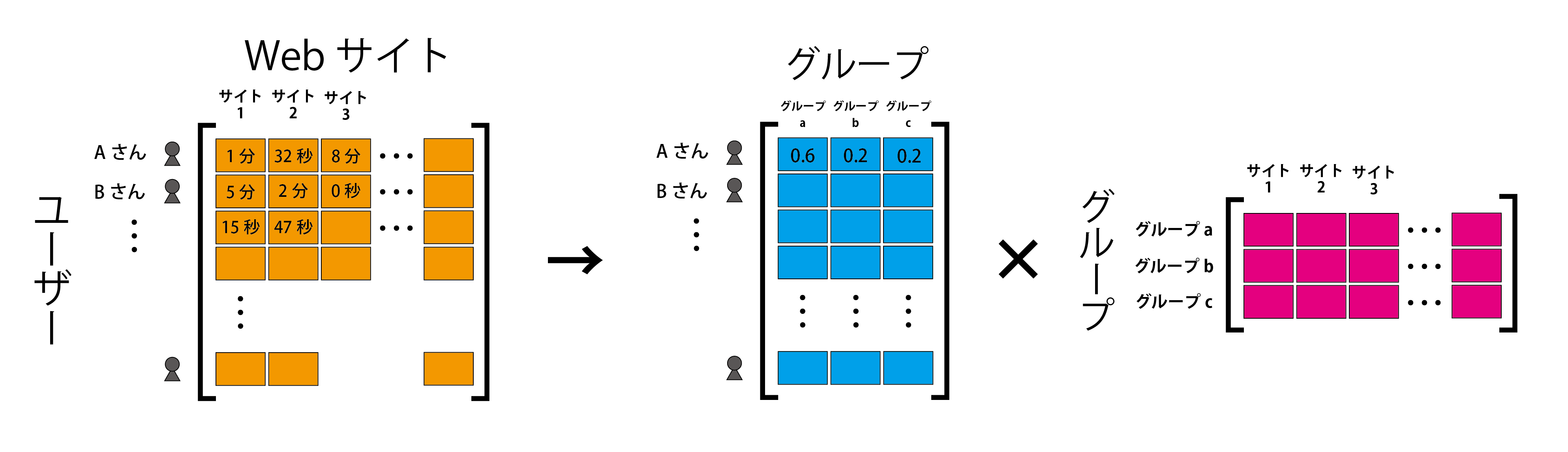
ここで注意すべきポイントは、あらゆる Web サイトの閲覧データを計算に用いているために、各ユーザーの長期的な興味 (平均的な興味)しか推測することができないということです。効果的な提案を行うためには、各ユーザーのその時その時の Web サイト毎の興味を推測する必要があります。しかし、この行列分解で得られた結果のみでは、それぞれの Web サイトを閲覧したときにどのような興味を持って訪れたのかまでは分かりません。
そこで吉田さんらは、上記の表の分割 (図2) により獲得された各ユーザーの平均的な興味の傾向を利用して、各 Web サイトに訪問した瞬間にどのような興味を持っていたのかを (グラフ理論のネットワークフロー問題に帰着して)数理最適化によって求めました。
ここでは、(2)「ユーザーがどの Web サイトからどの Web サイトへ移動したか」のデータを用います。あるユーザーの A さんが Web サイト 1 から Web サイト 2 へ移動したとき、(i)興味関心のジャンルを維持しながらWeb サイト 2 へ移動した場合と、(ii) Web サイト 1 を見ている間に興味関心が変わってWeb サイト 2 へ移動した場合の 2 つの可能性があります。例えば、ニュースサイトで政治関係の記事を見ていたとき、おすすめ記事でスポーツニュースが目に留まり、スポーツの試合の結果が気になってそちらのページに移動した場合は (ii) に該当するでしょう。(i) の場合、A さんは Web サイト 1 を見ている間も Web サイト 2 を見ている間も同じグループに所属しています。一方、(ii) の場合では、A さんは Web サイト 1 を見ている間と Web サイト 2 を見ている間で異なるグループに所属していることになります。Web サイト 1 から Web サイト 2 へ移動したユーザー全員を、以上のことに注意して整理すると、 (図3) のような図が描けます[5]。
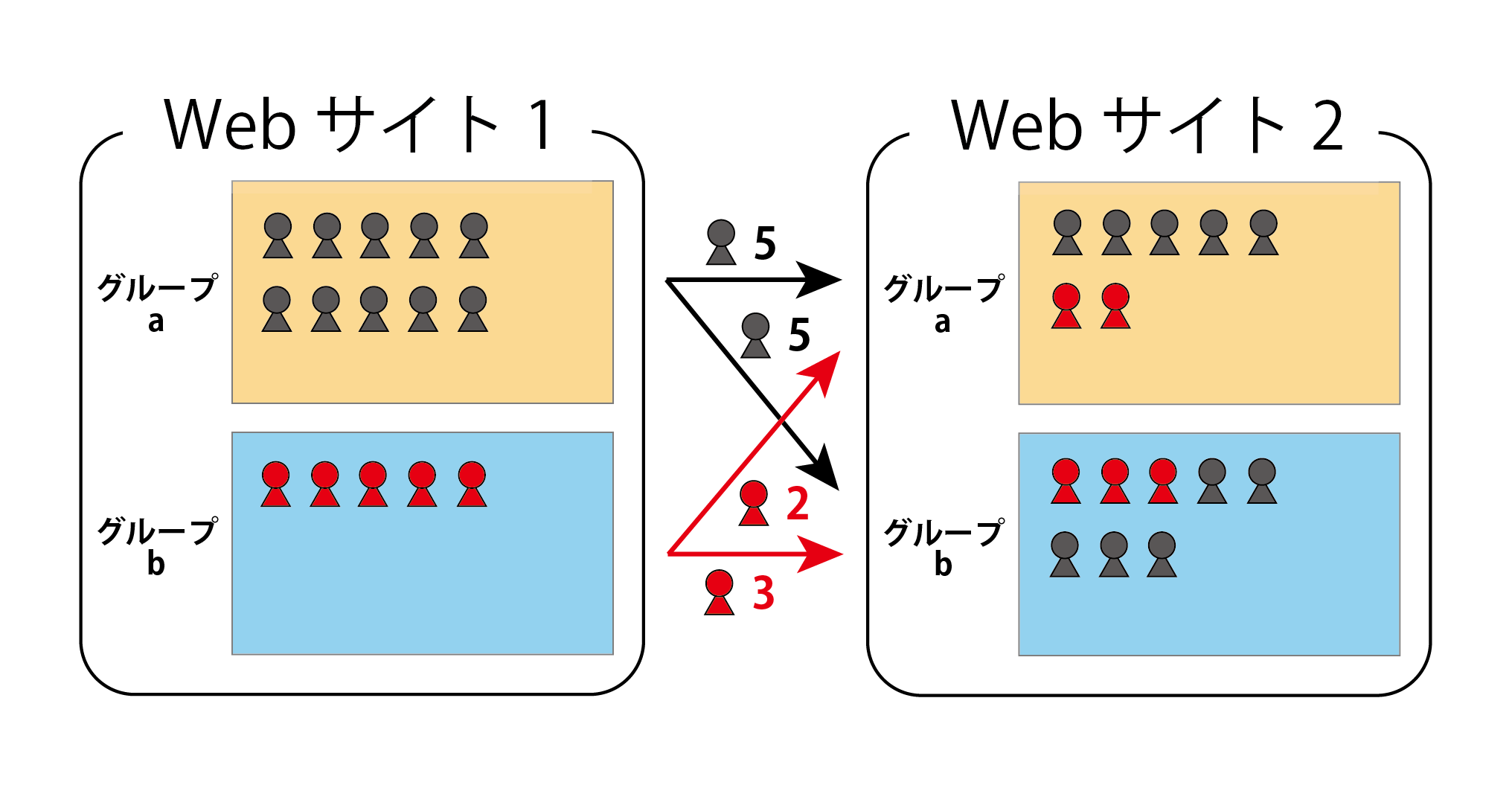
今、私たちが求めたい答えは、(図3) のような興味の移り変わりがある状況下での各ユーザーが各 Web サイトを閲覧している時に持っていた興味 (所属するグループ) です。これを数理最適化によって導くために、 いくつかの「できるだけ」満たして欲しい条件[6]を課し、これを用いて目的関数を設計します。例えば、
などです。また、人の出入りの数に矛盾が生じないようにするなど、「絶対」満たして欲しい条件も別途課し、これらを制約条件と言います。このように制約条件をいくつか課すことで、各ユーザーの興味の遷移方法を絞り込んでいきます。制約条件を満たす答えの候補の中から、目的関数を最大化 (もしくは最小化) させる答えを (もし存在すれば)見つけ出す数学的な手法を数理最適化といいます。
考えられる条件を数式により数理計画問題として表現する過程は大変ですが、楽しくて、やりがいを感じます。また、実運用のために、短い時間でコンピューターが数理計画問題を高速に解くことが求められる問題もあります。場合によっては、厳密解を短時間で求めることは諦めて、精度の良い近似解を現実的な時間で求めるアルゴリズムを開発することもあります数理最適化によって、(図2) から得られる平均的な興味ではなく、それぞれの Web サイトを訪れた瞬間の興味の種類を推測することができました。最後に、各グループに所属しているユーザーたちが、各 Web サイトでどのような行動をしているかを調べます。例えば、あるユーザーの A さんが、Web サイト 1 を訪問したときに、3 つの興味関心のグループ(a, b, c)に(0.5, 0.25, 0.25)という割合で所属することが、上記の数理最適化によって求まったとします。加えて、この A さんは、Web サイト 1 を 30 秒間閲覧したとします。このとき Web サイト 1 は、グループ a に所属するユーザー 0.5 人に 30 秒間閲覧されたとカウントします。同様にグループ b と c では 0.25 人分カウントします。全ユーザーに対して集計を行い、各グループに対して、横軸を閲覧時間、縦軸をユーザーの割合でヒストグラムを作ったものが (図4) です。このヒストグラムから、その Web サイトでは、グループ a、b、c に所属する人々がそれぞれどのような滞在をしたのかを知ることができます。例えば、(図4) の例では、グループ b は、閲覧時間が短いユーザーが大多数を占めていることがわかります。このことから、グループ b のユーザーは、その Web サイトにあまり興味がなく、すぐに離脱してしまったことが分かります。一方、グループ c では、閲覧時間がやや長いところで最大値を持っており、グループ c に所属する多くの人がこの Web サイトをしばらく閲覧したことが分かります。このことから、この Web サイトはグループ c のユーザーから興味をもたれたことが推測されます。以上のように、(図4) のグラフの形状は Web サイトの魅力を評価できる情報を含んでおり、それを数値で評価するために、次に説明するワイブル分布を利用します。
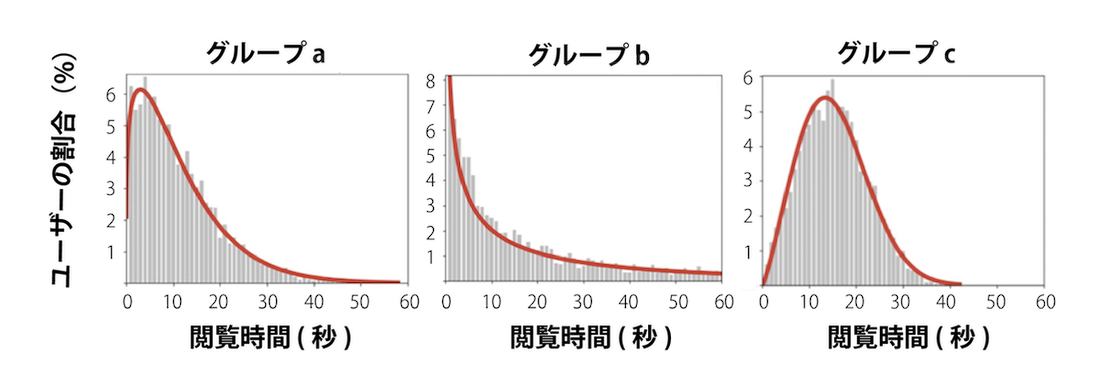
(図4) のグラフの形状を特徴づけるために、特定の関数を使って、形状を近似します[8]。それにより、その関数の性質を利用できます。吉田さんらの研究では、ワイブル分布を用いて関数の当てはめを行いました。ワイブル分布は、材料の強度や機械の部品の故障などを表す分布として、工学分野では信頼性解析の文脈で広く利用されています[9]。(図5) は、形状パラメータと呼ばれるパラメータmが、1 より大きい場合、1 に等しい場合、1 より小さい場合の 3 種類についてグラフが描かれています。注目すべきは、m < 1の場合のグラフは、(図4) のグループ b のグラフの形状と似ており、m > 1の場合のグラフは、(図4) のグループ c のグラフの形状と似ていることです。すなわち、ワイブル分布のパラメータmが、Web サイトが各グループからどれほど興味をもたれているかを表すのに便利な指標であることが推測できます。
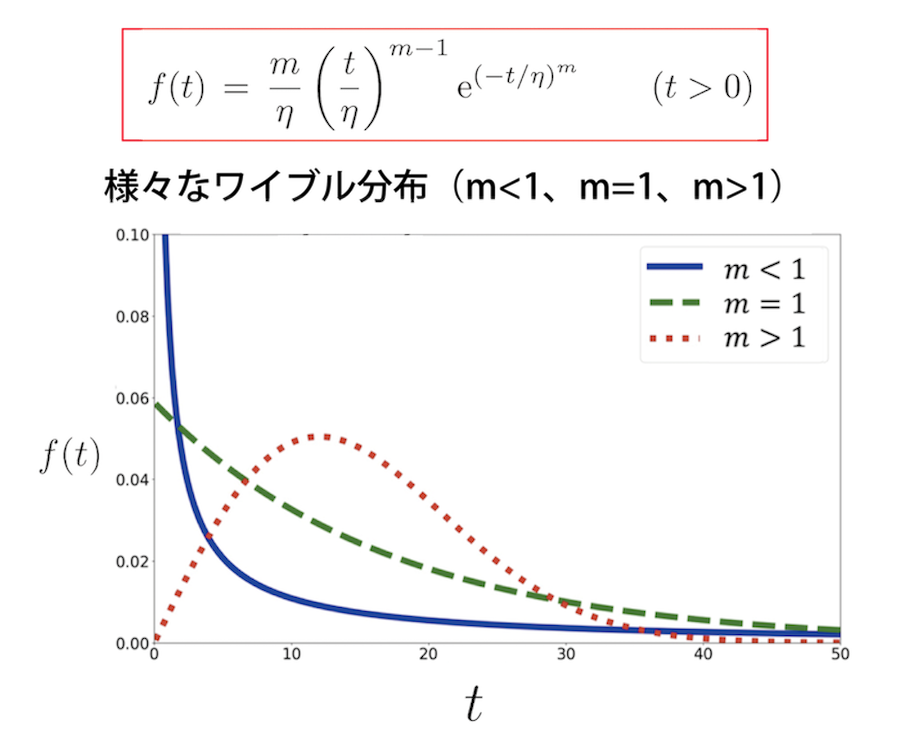
吉田さんらは、ワイブル分布の特性を考慮して、ワイブル分布の形状パラメータmが 1 より十分大きいグループが存在していて、かつ、そのグループに所属しているユーザーが多いほど、人々にとって魅力的な Web サイトであると考えました。このような考えをもとに新しい評価指標、Attractiveness Factor (魅力度) を提案しました。グループに所属するユーザー数は少なくてもmがかなり大きい値であれば、Attractiveness Factor は大きな値になります。アクセス数は少なくても、訪問するユーザーは皆その Web サイトに長時間居続けるならば、とても魅力的な Web サイトだからです。一方、目次ページやカテゴリーページなどは、非常に多くの人々が訪れますが、ユーザーはすぐに別のページに移ってしまうので、mは 1 よりも小さく、Attractiveness Factor では低い評価になります。
こちらの解析手法は、Yahoo! Japan の実際の Web アクセスデータに対して実験的に実行されました。さらに、従来の指標では解釈することが難しかった、人々の興味・関心に関する本質的な情報を取り出すことができそうだということも分かりました。
本研究は、ヤフー株式会社との共同研究として行われたものです。他にも多くの企業との共同研究を通して、数学を専門とされていない方とのコミュニケーションが必要な場面も多く、専門的な内容を平易な表現を用いて説明する技術が鍛えられました。
また、私たちの研究室では、数学科の中では (恐らく) 珍しく、チームプロジェクトとして 1 つのテーマを複数の学部生・大学院生と共に研究しています。私は本研究のプロジェクトリーダーとして研究を進めました。その際、メンバーをまとめる機会が度々あり、リーダーとしてのマネジメントスキル等を身に付けることができました。加えて、他の様々な研究プロジェクトにも参加しており、様々な産業での数学を活用した研究に携わることができています。現在の情報社会 (Society 4.0)[10]では、人々がサイバー空間 (仮想空間) へアクセスし情報を入手しています。一方、近い将来目指すべき社会の姿として、超スマート社会 (Society 5.0) が提唱されています。これは、フィジカル空間 (現実空間) のセンサーから膨大な情報 (ビッグデータ) をサイバー空間へ集め、人工知能 (AI) などを用いて解析した後に、フィジカル空間へフィードバックするという仕組みをもつ社会です。簡単な言葉で言い換えると、情報や人々の動きなどのビッグデータを解析し、最適な改善策を AI などにより見出して、それを実行することでより便利な社会にしよう、ということです。この社会の実現によって、我が国が抱える様々な課題の解決にも繋がると考えられています。吉田さんらの研究は、この超スマート社会の実現に直結するものです。
このような研究は、社会に役立つという実感が非常に大きいので個人的にはとてもやりがいがあります。今後は、人々の疲労度合や心理状態を Web アクセスデータから検出して、ストレス軽減に役立つようなコンテンツの提案が行えるように、研究を発展させていきたいそうです。将来的には、このような研究とビジネスの橋渡しをしたいとも考えているそうです。
私がプロジェクトリーダーを務めた研究は、他に自転車シェアリングサービスの再配置最適化の研究があります。というわけで、こちらのお話も少し伺ってみましょう。
最近、市街地の様々なところで、自転車や傘などのシェアリングサービスを見かけます。スマホや交通系 IC カード等があれば、料金を支払うことで簡単に借りることができ、また目的地で返却もできるため非常に便利です。しかし、これらのサービスを提供する上で課題があります。それは、シェアリング対象のもの (本研究では自転車) の使用傾向が極端に偏っていた場合、利用できないという問題が生じることです。例えば、自転車を借りようとサイクルポート (駐輪設備)[11]へ向かっても、空車の場合には借りられません。反対に、自転車を返却しようとしたときに、駐輪場が満車の場合は返却することができません (図6)。自転車を借りたくても借りられないという状況は、利用者とサービス提供者の両者の観点からみても機会損失です。この状況で適切にシェアリング対象のもの (本研究では自転車) を再配分する問題を再配置問題と呼びます。吉田さんらは、この再配置問題に対しても数学を用いて解決しようとしています。
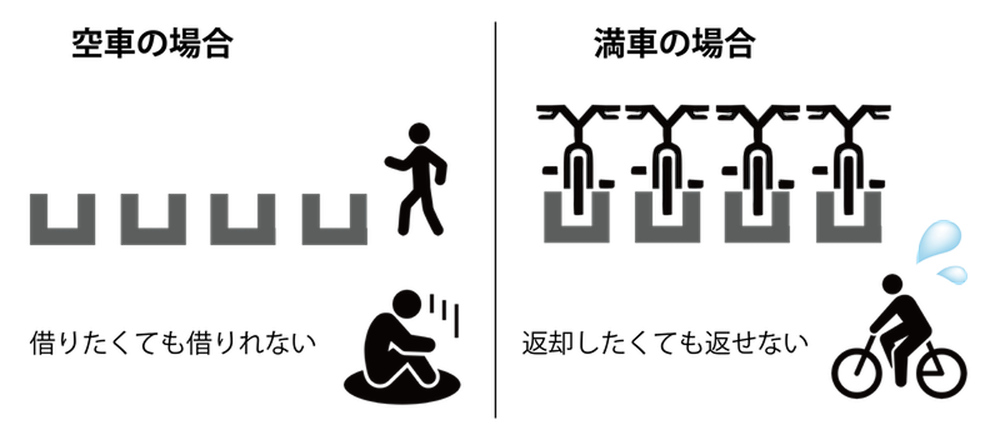
この課題を解くために吉田さんらは、深層学習と数理最適化の技術を組合せてアプローチしました。まず、各設置場所に将来何台自転車が利用 (貸出・返却) されるかという問題を 深層学習 (ディープラーニング) で予測しました。次に、(1) 機会損失を防ぐために各設置場所に何台自転車を配置すべきかを求め、(2) 実際にトラックを用いて自転車の再配置を行う際に、どのような順番で駐輪場をまわると効率がよいか、という問題を数理最適化により解きました。最後に、自転車の総数やサイクルポートの数、そして自転車のトラック輸送についての制約条件などを課して、最終的な配送経路を算出します。ただし、この最適化問題を厳密解で求めようとすると、かなりの計算時間がかかってしまうそうです。そこで、吉田さんらは、近似解を高速に求めるアルゴリズムを開発しました。
社会に結びついた研究では、トラックの運転手さんなど研究結果を利用する人に分かりやすいように可視化することや、現場の方々のフィードバックを受けてアルゴリズムを改善することも重要です。最近では、新型コロナウイルスの影響で自転車の需要が高まっており、特に公共交通機関を使わず遠方まで自転車で移動する人が増えています。そのため、より広範囲なエリアでの計算もできるように改良していきたいと考えているそうです。また、このような配送計画問題の需要は非常に大きく、今回の研究成果及びその過程で得た知見を活かして他の配送計画問題の研究にも取り組んでいるとのことです。
研究室に所属し、様々な研究に携わる中で、幅広い産業・社会課題に取り組める数学の力をひしひしと感じています。AIブームで深層学習・機械学習に大きな注目が集まっておりますが、様々な制約の下で意思決定をサポートする数学としての側面も持つ数理最適化にも関心を持って頂けると嬉しいです。
Note:
より詳しく知りたい方は・・・