

遺伝子は、しばしば「生命の設計図」とも呼ばれるように、そこに書かれた情報をもとにタンパク質が合成され、生物の様々な性質や機能が現れています。そのため、どの遺伝子が作用して、どのような性質 (形質) が現れているのかを同定することができれば、体質や病気のかかりやすさなどを調べることができます。しかし、この同定には、いくつかの難しいポイントがあります。まず、調べるべき遺伝子の数が現実的な測定データの数を大きく上回ってしまうこと、そして、遺伝子は他の複数の遺伝子と相互作用して、複雑に関係しあっていることです。そこで、沖永悠⼀さん (研究当時、数理学府数理学専攻 廣瀬研究室 修⼠課程) と九州⼤学マス・フォア・インダストリ研究所の廣瀬慧准教授は、⿓⾕⼤学農学部の永野惇准教授、 兵庫県⽴⼈と⾃然の博物館の京極⼤助研究員、トヨタ自動車株式会社の近藤聡⽒との共同研究で、相互作用する遺伝子の繋がりを考慮した擬似的な測定データをランダムに生成し、どれほどの測定データがあれば十分な精度で遺伝子の同定が可能かを計算しました。この研究成果は、Scientific Reports に掲載されています。
私たちの体は非常にたくさんの細胞からできています。その細胞の中には有名な二重らせん構造 (図1) をもつ物質の DNA (デオキシリボ核酸) が含まれており、DNA 内の 4 種類のヌクレオチドという物質 (アデニン、グアニン、シトシン、チミン) の並び順 (塩基配列という) によって表される情報のことを遺伝子といいます。この遺伝子の情報をもとに、まずメッセンジャー RNA (mRNA) というものが作られ、さらに mRNA に書かれた情報から様々なタンパク質が合成されます[1]。最終的に、このタンパク質のはたらきを通じて、生物の様々な性質や機能 (形質) が現れています。この形質は、私たち人間で言えば、体質や病気のかかりやすさなどです。植物ももちろん遺伝子を持っていて、農作物であれば害虫に対する抵抗力や収穫量などが形質として現れています。昨今では、このことを応用し、遺伝子を調べて形質を予測することで、医療や品種改良などに役立てようという技術開発が進んでいます。

遺伝子はそれぞれの個体固有のもので、一人の人であればどの細胞から遺伝子を取り出しても同じ配列をしています。一方、外部からの刺激やどの組織の細胞かによって作用する遺伝子は異なるため、同じ個体であっても合成される mRNA はいつも同じとは限りません。様々な状況下で、どの mRNA が合成されているかを調べることで、遺伝子と形質の関係を調べようとする研究手法は、トランスクリプトーム解析と呼ばれています。
遺伝子の数は膨大であるため、遺伝子と形質の関係を同定するためにはコンピュータを用いるのが便利です。そのためには、先ほど言葉で説明した関係を数式で表さなければなりません。現れる形質を \(y\) (例えば、病気のかかりやすさを 0 から 100 までで数値化したものと考えてください)、\(p\) 個の遺伝子を \(x_1, x_2, \ldots, x_p\) とすると、一番簡単なのは
という関係式を仮定することです。ここで、\(\beta_1, \beta_2, \ldots, \beta_p\) は定数です。例えば、2 番目の遺伝子が作用して、それに対応する mRNA が合成されると、\(x_2\) の値が大きくなり、それに合わせて形質 \(y\) の数値が変化する[2]、というような関係式です。
ただし、私たちは \(\beta_1, \beta_2, \ldots, \beta_p\) がどんな値をもつのか知りません。\(\beta_1, \beta_2, \ldots, \beta_p\) の値の大きさや正負が、その遺伝子が形質に対して有利にはたらくか、または不利にはたらくかを決めているので、\(\beta_1, \beta_2, \ldots, \beta_p\) が私たちの知りたい数値ということになります。トランスクリプトーム解析で得られる測定データは、\(y\) と \(x_1, x_2, \ldots, x_p\) の組です。異なる個体や異なる外部刺激を与えた状況で測定した \(n\) 個のデータがあったとして、\(i\) 番目の測定データを \(y^{(i)}\) と \(x_1^{(i)}, x_2^{(i)}, \ldots, x_p^{(i)}\) とすると、\(\beta_1, \beta_2, \ldots, \beta_p\) を求めるということは、
という連立方程式を解くことに対応します[3]。この連立方程式は \(p\) と \(n\) が同じ数であれば簡単に解くことができます[4]。しかし、現実のトランスクリプトーム解析では、遺伝子の数 \(p\) が数千から数万になるのに対し、測定データの数 \(n\) はそこまで増やすことができません。このような問題は「large \(p\) small \(n\) 問題」などと呼ばれ、解を求めるには工夫が必要であることが知られています。
測定データの \(y\) と \(x\) が分かっていて、そこから \(\beta\) を求めるという問題は、私たちの生活の中で普段からよく考えているかもしれません。何らかの実験データ、もしくは気温とアイスクリームの売上の関係[5]のようなものでも構いませんが、(図2) の左図 [A] の青色の点のようなデータが得られたとします。これらの測定データは全体的に右上がりの傾向にあるので、(図2) の左図 [A] の赤色の直線のような関係があるのではないかと考えたくなります。このように、測定データからどのような直線 \(y = \beta x + \alpha\) を引くかという問題が、まさにトランスクリプトーム解析で得られたデータから \(\beta_1, \beta_2, \ldots, \beta_p\) を求めることと同じです。測定データを直線の式 (一次関数) に当てはめることを線形回帰といい、測定データの点と直線の間の距離が小さくなるように直線 \(y = \beta x + \alpha\) を決定します (図2 [A])[6]。
![クリックやタップで拡大 <dfn class="fig">図2</dfn>:<span class="qrinews-figure-title">回帰分析の例</span> <b>[A]</b> 15 個の測定データを 1 次関数で表した場合。<b>[B]</b> [A]と同じ測定データを 10 次関数で表した場合。グラフは、記者がプログラミング言語の Python を用いて計算し、測定データは y=x に誤差を加えたものをランダムに生成した。](images/210819/fig2-28ac619b.png)

遺伝子と形質の関係は、単純な \(y = \beta x + \alpha\) という式では表されておらず、説明変数と呼ばれる、直線の式でいう \(x\) に相当するものが、\(x_1, x_2, \ldots, x_p\) の \(p\) 個あります[7]。これに似た状況は、例えば (図2) の右図 [B] の赤色の曲線で示されているような、[A] と同じ測定データを 10 次関数に当てはめるような場合です[8]。これを見ると、測定データの青色の点と赤色の曲線が、直線の式で当てはめた場合よりも良く一致していて、良い関係式が得られたのではないかと思ってしまいます。しかし、このぐにゃぐにゃの線に何か科学的な意味があるとは思えませんし、\(x = 4\) や \(x = 5.5\) に新たな測定データが追加されたとき、それらは赤色の曲線から大きく外れる可能性があります。この現象は過剰適合や過学習として知られ、説明変数の数 \(p\) に比べ、測定データの数 \(n\) が十分多くない場合に生じます。すなわち、large \(p\) small \(n\) 問題である、遺伝子と形質の関係を求める際にもこのことに注意しなければなりません。
過剰適合の解決策を考えてみましょう。(図2) の右図 [B] の赤色の曲線を数式で表すと、
というように係数が大きい数になっていることが分かります。一般に、過剰適合が起こる場合は \(\beta_1, \beta_2, \ldots, \beta_p\) が大きい値になってしまうことが知られています。そこで、説明変数を多数もつ回帰分析では、測定データと曲線の間の距離を小さくしつつ、一方で\(\beta_1, \beta_2, \ldots, \beta_p\) の値が大きくなりすぎないような曲線を求める、という手法がよく用いられます。これらのことに基づいて考え出された回帰分析の手法に、ラッソ回帰 (lasso)[9]や主成分回帰 (PCR)[10]があります。沖永さんらの研究では、この 2 つの方法を用いて遺伝子と形質の関係式を推定します。
ここまでは、遺伝子と形質の関係をどう求めるのかについて説明してきました。これに対し、沖永さんらはこの同定がどれほど精度良く決められているのか、用いる回帰分析の手法や測定データの数は精度にどれほど影響を及ぼすのかについて興味をもち、統計学などの手法を用いてこれを調べました。
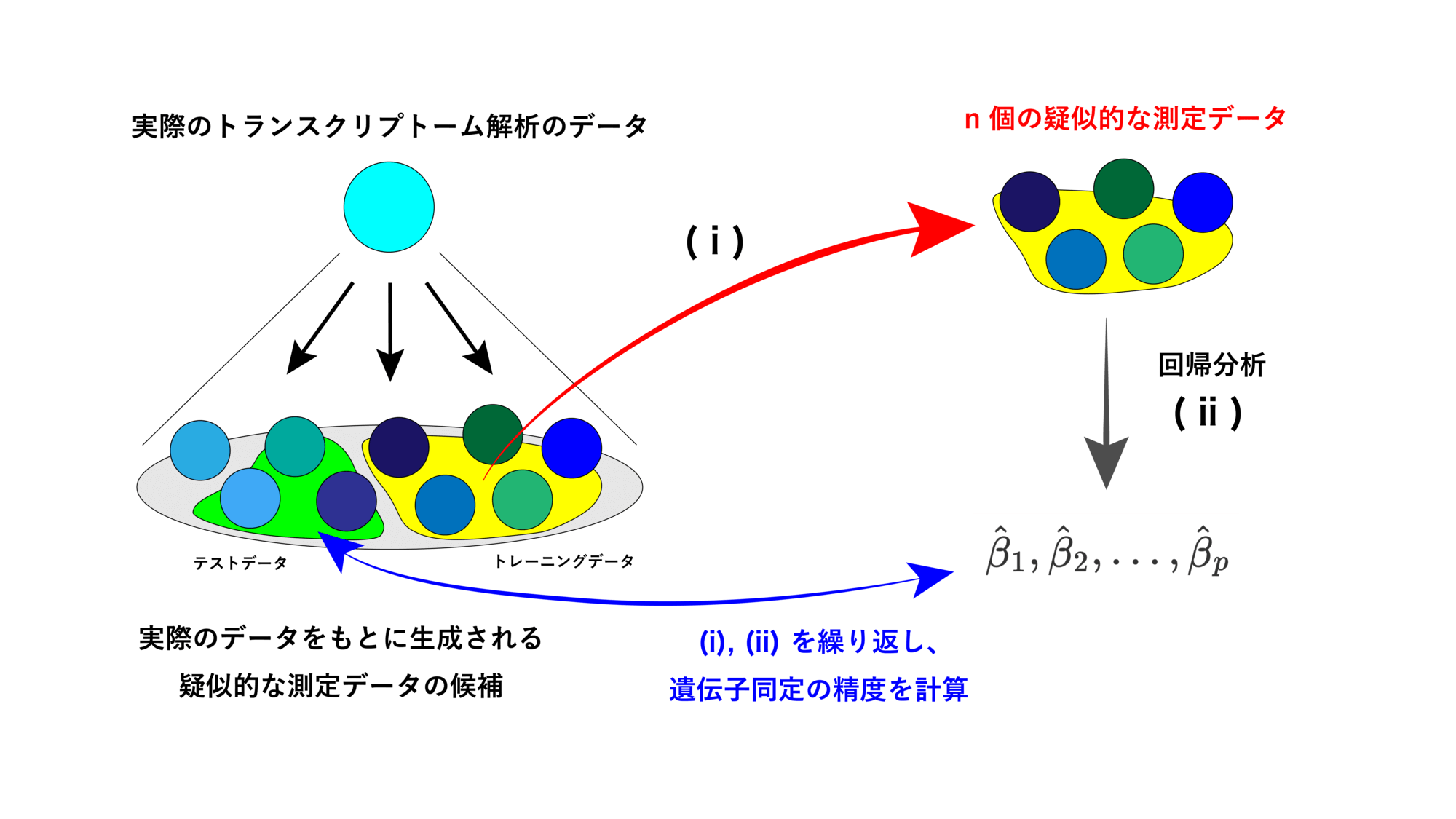
研究手法の大まかな流れは以下の通りです (図3)。まず、実際のトランスクリプトーム解析による結果、すなわち、測定データ \(y, x_1, x_2, \ldots, x_p\) と、それらの回帰分析によって得られた \(\beta_1, \beta_2, \ldots, \beta_p\) を用意します[11]。次に、これらのデータを基準にして、新たに擬似的な \(n\) 個の測定データをランダムに生成します。この擬似的な測定データに対して再度、ラッソ回帰もしくは主成分回帰を行い、\(\hat{\beta}_1, \hat{\beta}_2, \ldots, \hat{\beta}_p\) を求めます。元の \(\beta_1, \beta_2, \ldots, \beta_p\) とは少し違う結果が得られるはずなので、区別するために「\(\hat{\phantom{a}} \)」がついていることに気をつけて下さい。以上の ( i ) 擬似的な測定データの生成、 ( ii ) 回帰分析による \(\hat{\beta}_1, \hat{\beta}_2, \ldots, \hat{\beta}_p\) の決定、を何度も繰り返し、統計的な処理を行うことでどれほど精度良く遺伝子同定が行えるのかを計算します。

さらに沖永さんらは、
に着目し、これらが遺伝子同定の精度にどれほどの影響を及ぼすのかを調べました。最後に (3) について軽く触れた後に、沖永さんらの研究成果の一部をご紹介します。
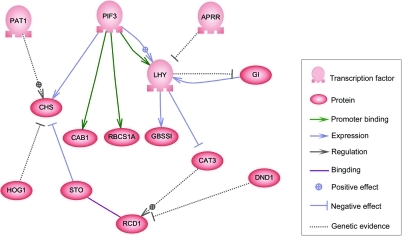
はじめに遺伝子の情報をもとにタンパク質が合成されると述べましたが、この仕組みは別のタンパク質 (転写因子という) によって制御されています。この転写因子はさらに、別の遺伝子の情報をもとに合成される場合があり、複数の遺伝子が複雑な因果関係をもっていることが知られています。この遺伝子の関係性を遺伝子制御ネットワーク (遺伝子調節ネットワーク) といいます (図4)。

タンパク質合成によって形質が現れるという仕組みの裏に、遺伝子制御ネットワークが内在していることは、トランスクリプトーム解析による測定データにも現れているはずです。例えば、2 番目と 3 番目の遺伝子が関係している場合、\(x_2\) の値が大きければ \(x_3\) の値もそれに応じて大きくなる、あるいは小さくなります。
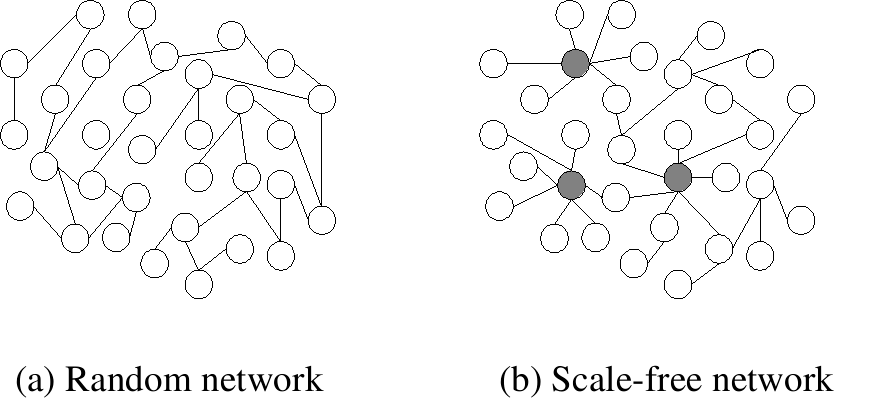
そのため、疑似的な測定データを生成する際も、このネットワーク構造に従って生成する方が、全くのランダムより、現実の測定データに近いものが得られると予想されます。そこで、沖永さんらは実際のトランスクリプトーム解析による結果をもとに、遺伝子制御ネットワークがランダムネットワークと呼ばれるタイプのネットワーク構造 (図5 (a)) をもつ場合とスケールフリーネットワークという構造 (図5 (b)) をもつ場合について考え、これらに従って疑似的な測定データを生成しました。比較のために 2 種類のネットワークについて研究が行われていますが、一般に遺伝子制御ネットワークはスケールフリーネットワーク(図5 (b)) に近いと考えられています。

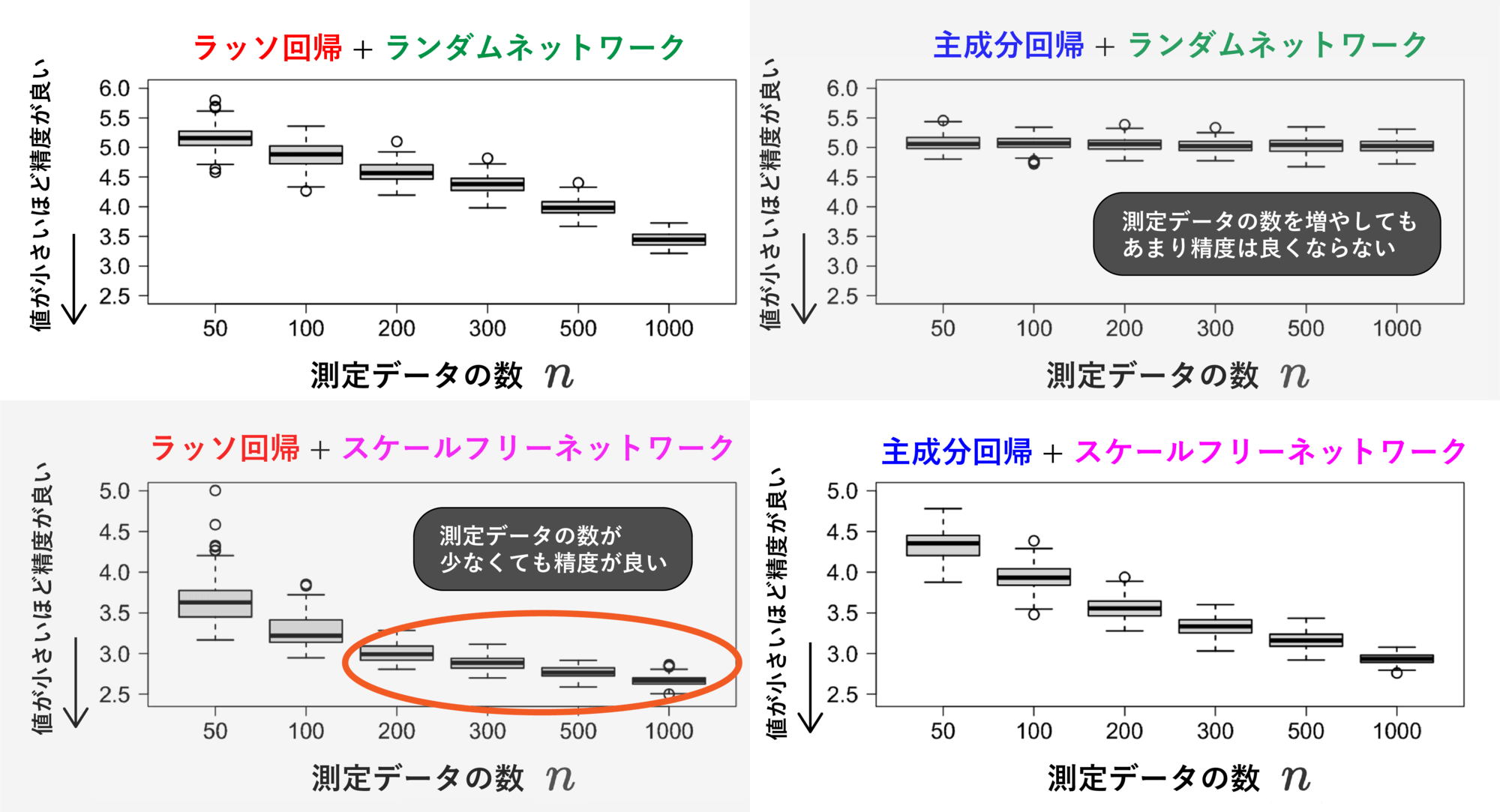
以上をもとに、遺伝子同定の精度を計算したものは (図6) に示されています。4 つのグラフは、回帰分析の手法や擬似的な測定データを生成したネットワーク構造が異なる場合を表していて、横軸は測定データの数nです。縦軸は、値が小さいほど遺伝子同定の精度が良いことを示しています。注目すべきは、スケールフリーネットワークをもつ対象に対してラッソ回帰を行う場合 (図6 左下) は、測定データの数が数百程度でも十分な精度で遺伝子同定が行えることです。一方、ランダムネットワークをもつ対象に対して主成分回帰を行う場合 (図6 右上) 、測定データを増やしてもあまり精度は良くならないことが分かりました。

 研究を進めていく中で、これまで学んだことがなかった多方面の専門的な知識が必要になる場面がたくさんあり、それらを理解するのに苦労しました。しかし、先生方のサポートのおかげで、今回の研究成果をあげることができました。
研究を進めていく中で、これまで学んだことがなかった多方面の専門的な知識が必要になる場面がたくさんあり、それらを理解するのに苦労しました。しかし、先生方のサポートのおかげで、今回の研究成果をあげることができました。遺伝子データのサンプリングはお金や手間がかかり、大量に取得することが難しくなります。この研究も、共同研究者の方々が少ない測定データで遺伝子同定を行わなければならなかったことが発端になっているそうです。今回の研究成果は、遺伝子同定を行う際に必要となる測定データの数をより正確に導き出す方法を見出すことにつながるだろうと沖永さんらは考えています。
 現在は、大量の遺伝子データをサンプリングできるような手法を開発する方が主流らしいのですが、少ない測定データでも高い予測精度が得られる手法を開発することも重要であると考えています。
現在は、大量の遺伝子データをサンプリングできるような手法を開発する方が主流らしいのですが、少ない測定データでも高い予測精度が得られる手法を開発することも重要であると考えています。ネットワーク構造は、身の回りの様々なところで見つけることができます。今回は遺伝子データを対象として研究が行われましたが、このような研究は、ネットワーク構造をもっていてサンプル数が限られる別の対象にも応用できるのではないか、と記者は感じました。
 R (統計分野で良く用いられるプログラミング言語の 1 種) を使ってシミュレーションを行ったことが楽しかったです。私が R を触ったのは学部 4 年生のときの研究がきっかけで、最初は下手なコードしか書けず、できることも限られていたのですが、だんだんとできることが増えていくのが実感できて、やりがいがありました。
R (統計分野で良く用いられるプログラミング言語の 1 種) を使ってシミュレーションを行ったことが楽しかったです。私が R を触ったのは学部 4 年生のときの研究がきっかけで、最初は下手なコードしか書けず、できることも限られていたのですが、だんだんとできることが増えていくのが実感できて、やりがいがありました。 論文の査読を通して結果の誤りが見つかり、時間のかかるシミュレーションを初めからやり直したこともありました。最終的に論文化されて、良かったです。
論文の査読を通して結果の誤りが見つかり、時間のかかるシミュレーションを初めからやり直したこともありました。最終的に論文化されて、良かったです。
Note:
より詳しく知りたい方は・・・