

ハイブリット車の開発現場では、モデルベース開発 (MBD) が主流となっています。MBD ではシミュレーション上に車を再現して、テストコースを走行させることで燃費性能を測ります。その際に、車の性能を最大限に引き出すようにシミュレータを制御することが重要となります。従来はシミュレータの制御法を人の手でチューニングしており、シミュレータの一つ一つに対して手作業で制御を最適化してきました。しかし、この方法にはかなりの時間がかかり、またシミュレータが新しくなるごとに再調整しなければならないという問題を抱えていました。そこで我々は、シミュレータ制御の最適化を「グラフ上の制約付き最短経路問題」という数学の問題に焼き直し、その問題を解くプロセスを自動化することで、従来よりも高速で汎用的なアルゴリズムを開発しました。研究成果は IFAC-PapersOnLine に掲載されました。
燃費がよく環境にもやさしい自動車として、ハイブリッド車が注目を集めています。ハイブリッド車とは、一般に 2 種類以上の動力源を持つ自動車を指しますが、日本でよく見かけるのは「ガソリンエンジン」と「電気モーター」を併用した電気式ハイブリッド車 (HEV) です。1997 年にトヨタ自動車が初代プリウス™ (図1) の販売を開始するのを皮切りに、現在では各自動車メーカーが HEV 車の開発・販売を精力的におこなっており、新車の 5 台に 1 台は HEV 車であるとまで言われています。
HEV 車の燃費性能は、パワートレインと呼ばれる動力伝達装置で決まります。近年ではモデルベース開発 (MBD) という手法が導入され、パワートレインの開発が従来よりもはるかに効率的になってきました。MBD とは「パソコンの中で車を再現し、試走させて燃費の良さを測るシステム」です (図2)。この手法を用いれば実機を作る前に性能をテストすることができ、膨大な試作候補からより燃費性能が良いパワートレインを絞り込むことができます。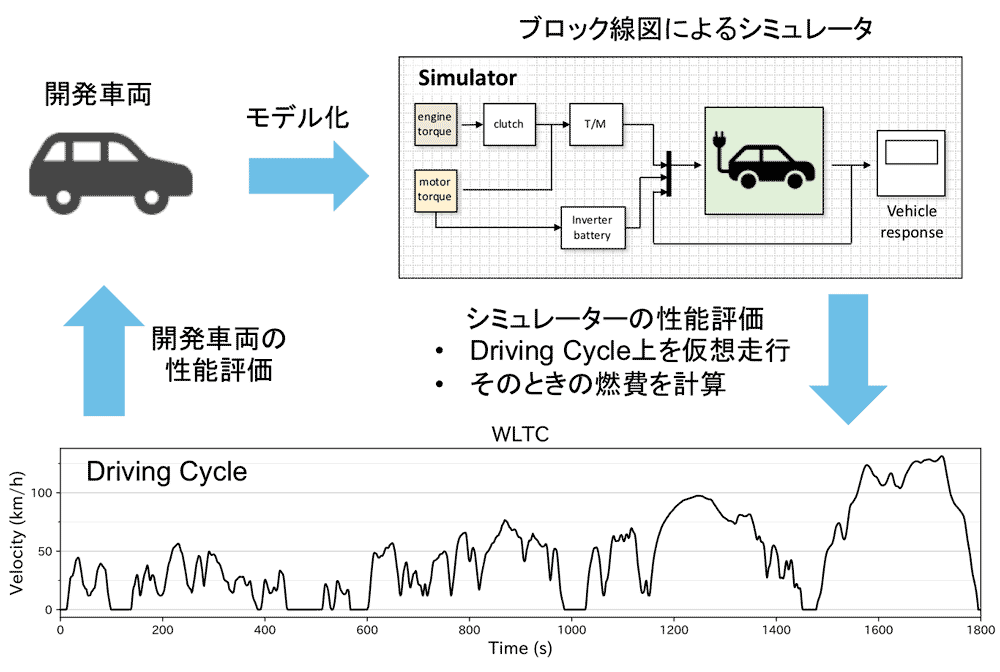

MBD の手順は次のとおりです。
とくに重要となるのが、(2) におけるシミュレータの制御法、言うなれば「ドライバーの上手さ」です。HEV 車ではエンジンとモータの上手な使い分け[1]が燃費に直結します。そのため、いくら性能がいいパワートレインを使っても、それを引き出すような制御ができなければ悪い評価を与えてしまいます。したがってパワートレインの性能を正確に評価するためには、シミュレータの性能を最大限に引き出すような制御法を求めることが必須です。
しかし、最適な制御法を見つけることは簡単ではありません。エンジンとモーターの同時制御だけでも複雑であるのに、バッテリーの残量にも気をつけなければなりません。エンジンの始動システムやエアコンなどの電子機器のために、最低限のバッテリーは残しておく必要があります。また、Driving Cycle 走行前後でバッテリー残量は等しくなければならないというルールもあります。これらの拘束条件が、制御法の最適化をますます難しくしています。
従来の方法では、人の手によるチューニングでこの困難を回避してきました。しかし、たった一つのパワートレインを調べるのに 2 〜 3 日もの時間がかかり、車両を変えるごとに調整が必要だという汎用性の無さが問題視されていました。新車の開発段階では大量のパワートレイン候補を評価しなければならず、またパワートレイン自体も年々複雑化している昨今、より効率的な制御法を自動的に見つけるしくみ (アルゴリズム)が求められています。そこで我々は、最適化の問題をグラフ上の制約付き最短経路問題という数学の問題に焼き直し、その問題を解くプロセスを自動化することで、従来よりも高速で汎用的なアルゴリズムを開発しました。
本研究の目標は、パワートレインを模したシミュレータに対して「効率的」な制御法を「自動的」に見つけるアルゴリズムを開発することです。そのためにはまず、シミュレータの制御を数学的に定義しなければなりません。
シミュレーションの内容は、ドライバーの頭の中とまったく同様です。私たちが運転するときには、ある一定時間ごとに車の状態を読み取って、次に加速や減速が必要ならばブレーキやアクセルを踏むか判断し、車を望ましい状態へと導いています。運転とはこの手順の繰り返しです。シミュレーションでも同じように Driving Cycle を分割して、各区間ごとに制御をおこないます (図3)。

シミュレーションにおける入力パラメータは「エンジンやモータのどちらを使うか、どれくらいの時間で駆動するか」や「シミュレータへの目標トルク値 (エンジンやモータが出す力)」であり、これのパラメータを区間ごとに変化させることで車両の状態を遷移させています。
効率のよい運転とは、燃料の消費をできるだけ抑えた運転だと考えられます。したがってシミュレータを効率的に制御するという問題は、「エンジンやモーターの駆動時間などを入力パラメータとして燃料の消費量を最小化する」という数学の最適化問題として捉えることができます。バッテリ残量などを一定以上に保つという制約もあるため、この問題は制約付きの最適化問題に分類されます。
この問題を解くのは一筋縄ではいきません。区間ごとに入力パラメータがあり、その組み合わせは無限に多くあるため、パラメータを総ざらいして最良の制御法を見つけることは不可能です。そこで我々は、数学的に保証された方法でパラメータの探索領域を減らし、計算の無駄を省きました。具体的には、各区間における車の状態遷移をグラフ[2]で表現し、考えている問題を「グラフ上の制約付き最短路を求める問題」で近似させました。
図4 (a) にグラフの一例を示します。グラフの各点は、図3 の各区間における車両状態に対応します。たとえば「HV モードがオンで、ガソリンが残りいくらで、充電残量がいくらで...」といったように定義されています。ある点から右隣にある点へ移ることは、ある区間から次の区間へと車両が移動することを意味します。
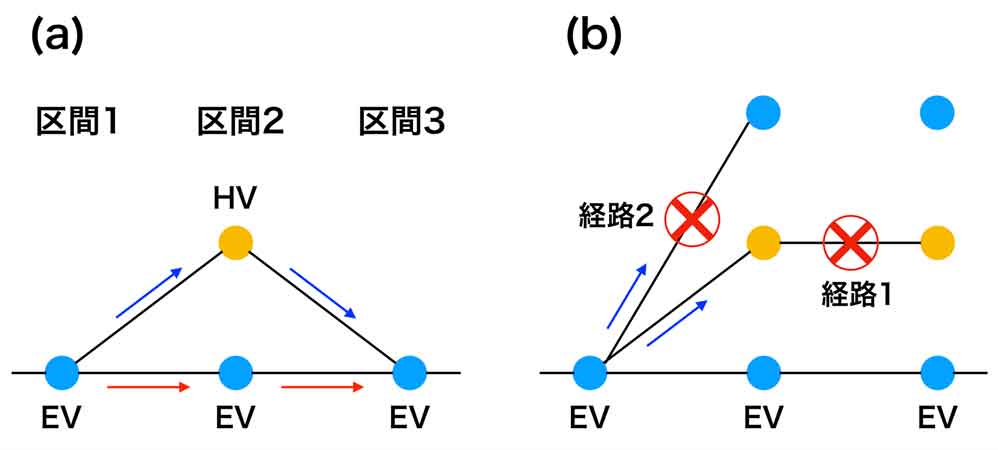
ここでポイントとなるのが「区間から区間へと順番に問題を解くことで、パラメータの探索領域を削減できる」ということです。なぜならば、ある点が定まると次に移れる点が絞り込まれるからです (図4 (b))。たとえば減速したい区間では、ガソリンを使うような点に移ることは許されません (経路 1)。またバッテリー残量をある程度残す必要があるため、EV モードから EV モードへの遷移も制限されます (経路 2)。このような制限を考慮しながら許される状態量遷移のパターンをいくつか計算してみると、図5 のようなグラフが得られました。
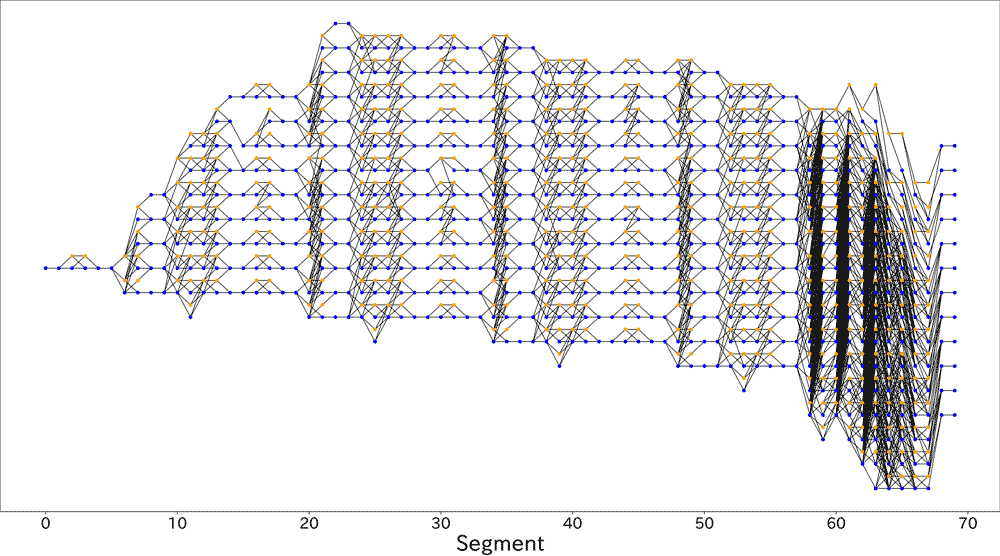

あとは各区間ごとの結果をつなぎ合わせたときに、最良となるようなつなぎ方を求めれば最適解を得ることができます。バッテリー残量を一定以上に保つといった条件が加わっているので、グラフ上の制約付き最短路問題を解くことになります。一般に、グラフ上の制約付き最短路問題は NP 困難[3]であることが知られています。この問題を効率的に解くアルゴリズムは知られていないため、計算には何らかの工夫が必要になります。そこで我々は 0-1 整数線型計画法により定式化をおこない、線型計画ソルバーと呼ばれるソフトウェアを用いて解いてみたところ、短時間で最適解を求めることができました。
我々の提唱したアルゴリズムは、4 つの STEP で構成されています (図6)。
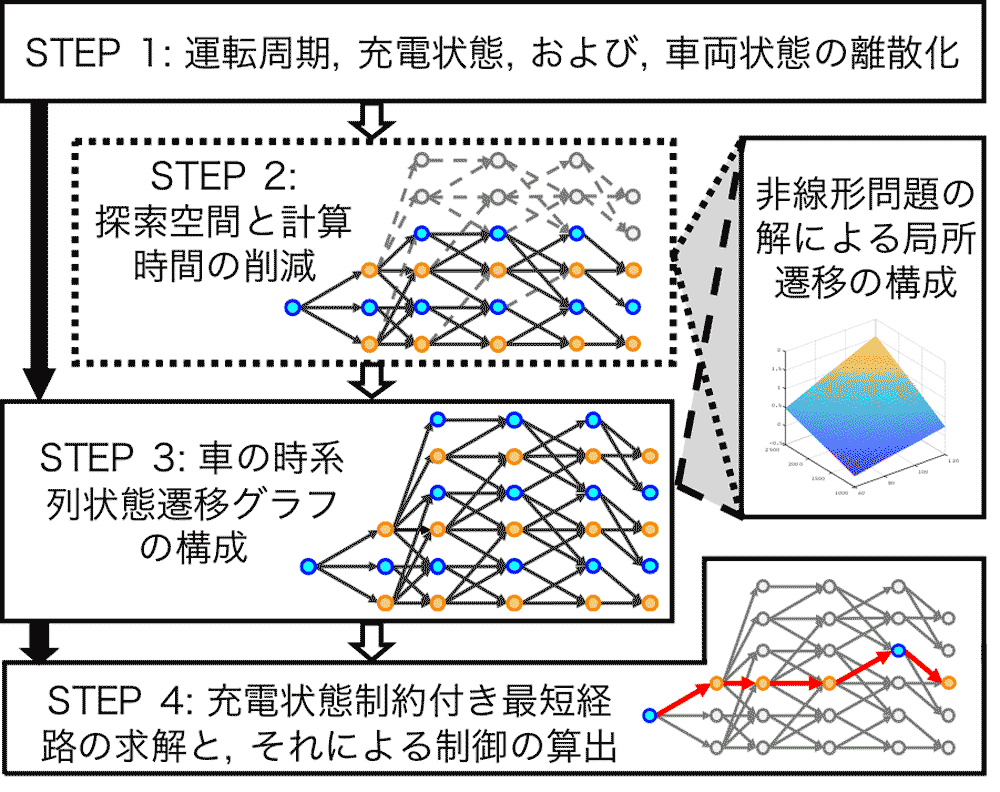
STEP 1 では入力パラメータを設定します。STEP 2 では車の状態遷移をグラフとして表現し、近似によって計算時間を削減します (詳しくはこちら)。STEP 3 ではグラフを構成します。最後の STEP 4 では構成したグラフ上で制約付き最短路問題を解きます。これらの工程は数学的に定義されており、コンピュータを使うことによって自動的に処理することができます。
トヨタ自動車様から提供していただいたハイブリッドシミュレーターを用いて、アルゴリズムの検証をおこないました。バッテリー残量の制約をうまく考慮できているか調べるため、今回は走行開始時のバッテリー残量が異なる 2 パターンを考えました (図7)。
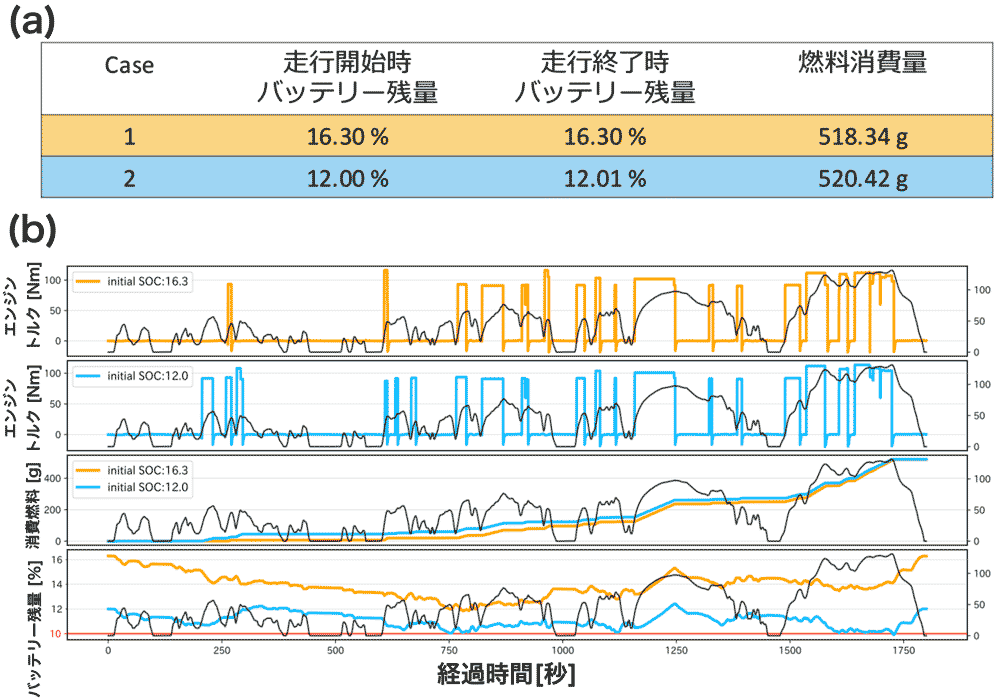

パターン 1 では走行開始時のバッテリー残量を 16.3% とし、パターン 2 では 12.0% としています (それぞれオレンジ色と青色で描写しています)。今回の検証では、バッテリー残量が 10% を下回らないように制限しています。図7 (b) における黒い線が Driving Cycle の速度データを表しています。
まず 図7 (a) のバッテリー残量に注目すると、どちらのパターンにおいても走行開始時と終了時のバッテリー残量がほぼ揃えられており、我々のアルゴリズムがうまく機能していることが見て取れます。
次に 図7 (b) にあるバッテリー残量の時間経過をみてみると、全体的なふるまいは 2 つのパターンでそれほど違っていませんでした。しかし、200 秒付近では明らかな違いが見られます。この時間帯での Driving Cycle を見てみると山なりになっており、この区間では加速から減速へと移っていることがわかります。加速時にはエンジンとモータのどちらを使うかという選択肢がありますが、パターン 1 ではモータを使い、パターン 2 ではエンジンを動作させていることが分かります。パターン 2 では開始時のバッテリー残量が 12% と少なく、モータを使うとバッテリー残量が 10% を下回ってしまうため、バッテリーを充電するために仕方なくエンジンを動作させていると理解できます。こういった加速・減速の頻ぱんな繰り返しは、街中を走るときによく見られます。したがって、我々のアルゴリズムによって繊細な制御を実現できたということは、生活スタイルに合わせた柔軟な制御へとつながる重要な成果です。
今回の計算で特に時間がかかった部分は、グラフにおいて各区間での枝 (車両の状態量遷移のパターン) を決定するところです。
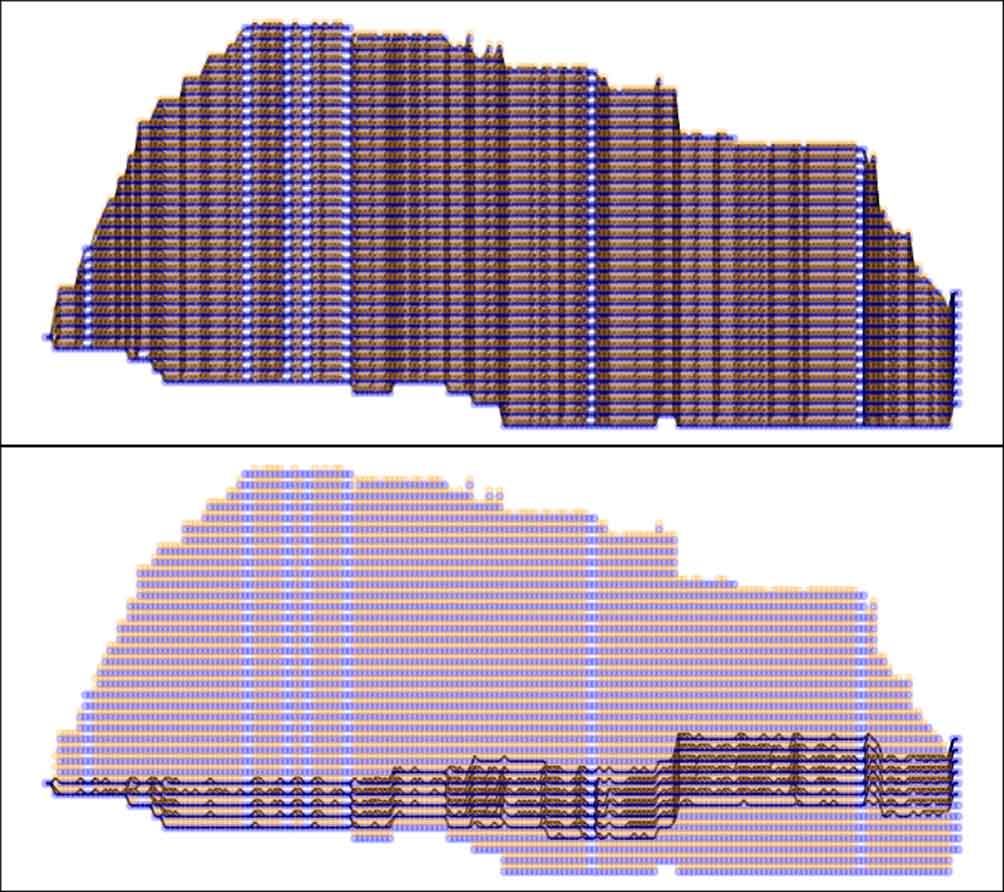

上のグラフがもともとのグラフです。解きたい問題を近似した部分問題を用いることで、不必要な枝の計算を省略するように工夫したところ、下のグラフが得られました。驚くべきことに 97.16% もの枝が削減されています。もちろん枝を削減する処理自体にも計算時間はかかるのですが、状態量遷移のパターン数が圧倒的に少なくなるので、アルゴリズム全体で 4 倍ほど処理時間を高速化することに成功しました。
今回の研究ではシミュレータの制御に注力してきましたが、将来的にはリアルタイムでの最適制御によってドライバーを補助することも視野に入れています。上記アルゴリズムにより、あらかじめ与えられた 1 時間程度の Driving Cycle 上の制御法を、5 時間ほどで計算できています。つまり、このアルゴリズムは将来 1 時間の速度変化の情報を入力してはじめて、その 1 時間分の制御法を計算することができます。一方、リアルタイム制御の場合には、将来の速度変化が分からない状況で制御する必要があるため、新たな拡張が必要となると考えられます。またドライバーによって運転の荒さなど特徴が異なるため、ドライバーに適した車両制御を見つけることにも興味があります。
制御理論やハイブリッド車の構造などは、ほぼ知らない状態から研究が始まりました。そのためトヨタ自動車の方と打ち合わせを重ねて、様々なことを教えていただきながら研究を進めていきました。
また研究室の先生や学生達と議論を行いながらアルゴリズムのアイデアを詰めていきました。数学は孤独な学問と思われがちですが、そうではない一面を感じることができました。
Note:
より詳しく知りたい方は・・・