九州大学 理学研究院 理学府 理学部

Advances in Engineering 社による評価

岩下助教らの研究が、Advances in Engineering (AIE) 社の注目論文として紹介されました (詳しくはこちら)。

AIE 社はカナダのリサーチ会社です。 工学系の学術雑誌からすぐれた研究成果を選び出し、民間企業へと紹介することで、マッチングやコンサルティングをおこなっています。特に注目すべき研究については、自社のホームページにて解説記事を掲載しています。岩下助教らによる研究が AIE 社に注目されたということは、本研究成果が工学分野への応用と実用化が期待される重要な成果であることを示しています。以下の記事にて研究の詳しい内容をご紹介いたします。

研究の動機

コロイド粒子と私たちの生活

原子・分子より大きく細胞くらいには小さな粒子 (直径 10 ㎚ ∼ から数 ㎛) を総称して、コロイド粒子 “coloidal particle” と呼びます。コロイド粒子は私たちの身の周りにあふれています (図1) 。

牛乳のタンパク質や脂肪は、コロイド粒子の一種です。豆腐や寒天は、コロイド粒子系がゲル化したものです。他にもインクや化粧品などの工業製品にはじまり、細胞や血液などの生物の要素、オパールなどの鉱物、さらには煙や霧などの自然物に至るまで、これらはすべてコロイド粒子から構成されています。したがって、コロイド粒子が寄り集まって凝縮するメカニズムを明らかにすることは、物質のなりたちを理解するための根本的な課題です。

異方的コロイド粒子の研究は始まったばかり

これまでのコロイド研究では、主に「等方的」コロイド粒子を扱ってきました。一方で、現実のコロイド粒子はさまざまな形をもち、多様な表面物性を示します (図2)。このような「異方的」コロイド粒子の研究が、近年盛んにおこなわれています。最近の研究によると、異方的コロイド粒子系では「等方的」な系には存在しないような新規で多彩な凝縮構造が見つかっており、「異方性」から秩序が生み出されるメカニズムへと注目が集まっています。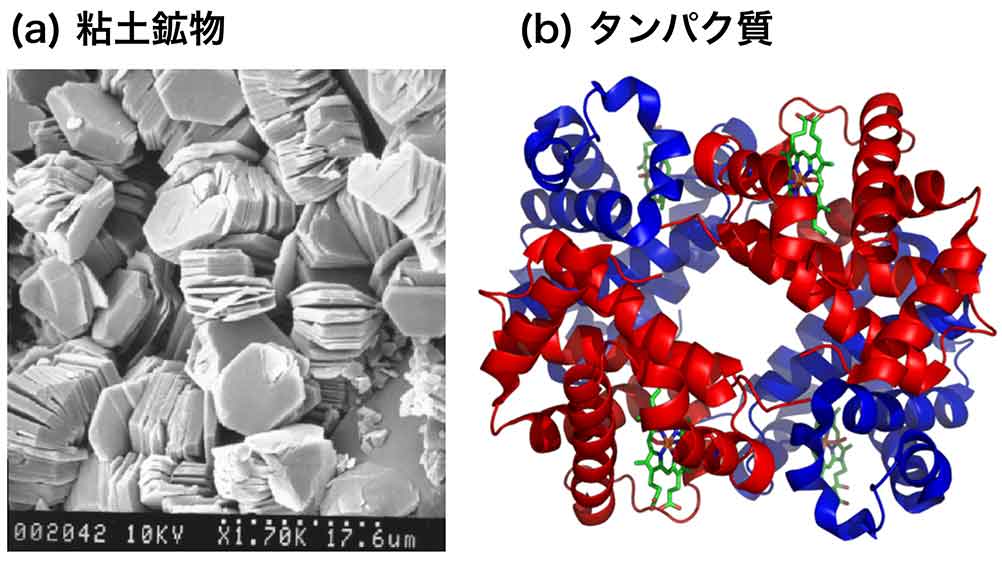

しかしながら、異方性の本質を捉えることは一筋縄ではいきません。一口に異方性といってもさまざまな要因があり、粒子の形や表面物性など多種多様です。また実験的に異方性を制御することは難しく、等方的な系にくらべて実験例はごく少数です。そのため、凝縮構造の体系的な理解にはほど遠いという現状があります。

パッチ粒子で探る「異方性」の本質

そこで岩下助教らは、シンプルな異方性をもつコロイド粒子としてパッチ粒子 “patchy particle” に着目し、パッチ粒子系を系統的に調べることで異方性の本質を明らかにしています。パッチ粒子とは、表面に物性の異なる領域 (パッチ) をもつコロイド粒子です。パッチの個数や配置を変えることで、パッチ粒子に色々な異方性を与えられるため、パッチ粒子系は異方的コロイド粒子系のモデル系だと考えることができます。

今回の研究では、粘着性のある 1 パッチ粒子系に着目しています (図3)。この系ではパッチ間に引力がはたらいており、パッチ粒子が自己組織化 “self-assembly” ^[1]することで多彩な構造を作ります。パッチ粒子が一塊となって運動するクラスター “cluster” が現れたり、パッチの向きに方向秩序 “orientat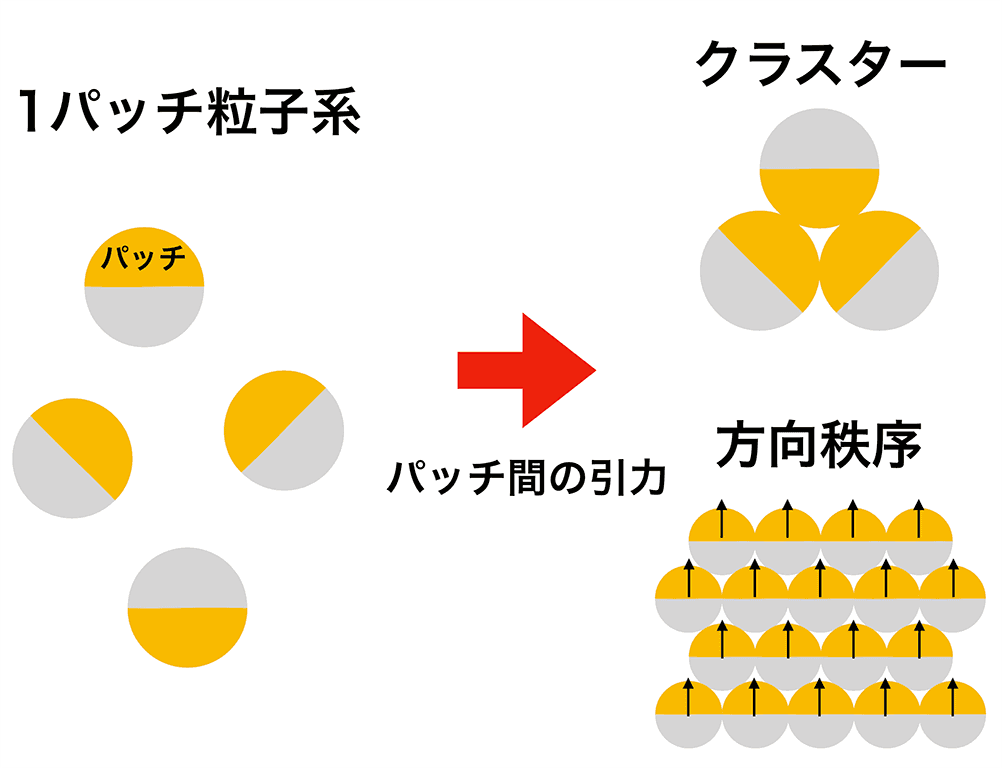inal order” が現れたりします。

岩下助教らのこれまでの研究では、1 パッチ粒子を平行板に閉じ込める実験をおこない、クラスターや方向秩序の形成を実証してきました (図4)。たとえば、パッチの向きがジグザグに揃うストライプ構造 (図4, ZS) や、6 つの粒子によるクラスターが規則的に並んだハチの巣模様 (図4, O) などを観測しています。またパッチサイズや平行板の幅を変えるだけで、凝縮構造が劇的に変わることを明らかにしてきました。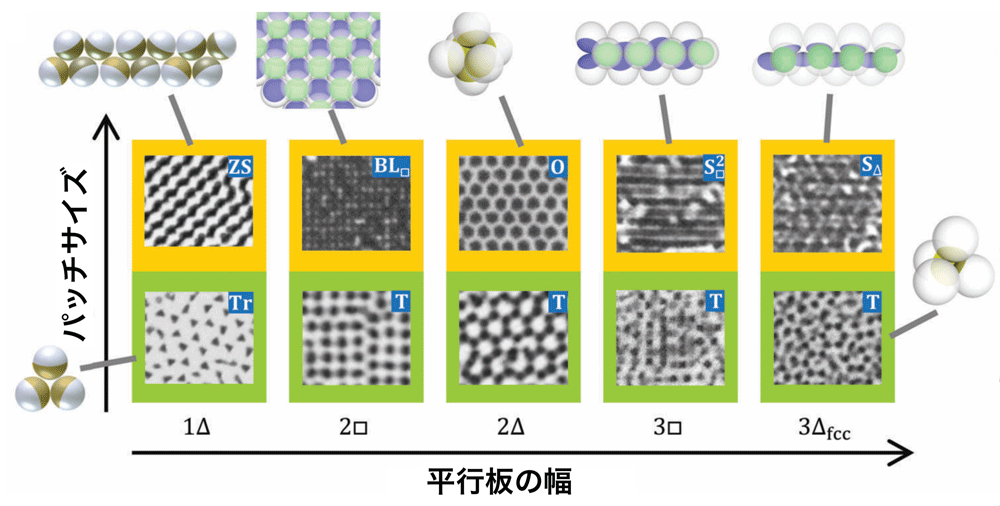

このようなパッチ粒子の自己組織化は、ナノテクノロジーの分野に応用できます。高い強度をもつ素材や高効率な触媒に必要とされる微細で複雑な構造をパッチサイズやパッチの配置を工夫するだけで実現できる可能性があります。

凝縮構造が生まれるメカニズムとは

以上のように、非常にシンプルな異方性をもつ 1 パッチ粒子系においてさえ、実に多様な方向秩序やクラスター構造が現れます。これほどにバラエティ豊かな構造はどのようなメカニズムで生み出されるのでしょうか ? また異方性はどのような役割を果たしているのでしょうか ? 今回の研究ではこれらを謎へと迫るべく、これまでほとんど調べられてこなかった密充填から分散状態までのさまざまな密度における 1 パッチ粒子系を観測しました。

実験の内容

1 パッチ粒子の作り方

1 パッチ粒子の分散系を作ります。シリカ粒子を基盤上に並べて、金のガスを吹き付けることで、半球面が金で覆われたパッチ粒子を作製します。このパッチ粒子を 図5 (a) のようにエッチング液 (金を腐食させる液) に浸してパッチサイズ θ_ap を調整します。金パッチの表面をイオン性チオール “ ” ^[2]で保護し、パッチ粒子を特殊な媒質 “ ” ^[3]へ混ぜ入れると、パッチ粒子を数日間は分散させることができます。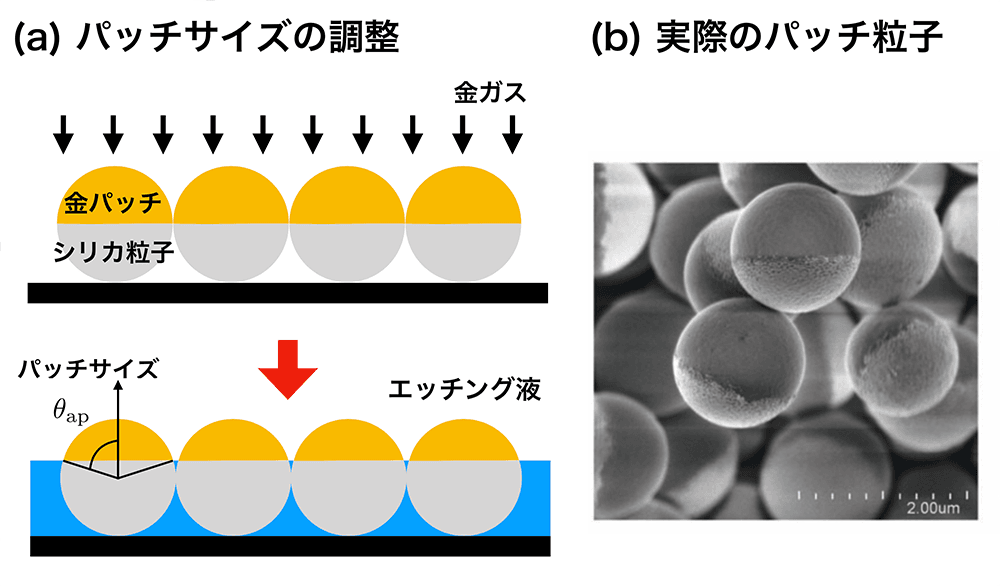

パッチ粒子を密に詰め込む

次に、パッチ粒子を密に詰め込みます (図6)。溶液をクサビセルに入れて、30 分ほど遠心分離機にかけます。容器を傾けて数時間ほど置いておき、重力によってさらに詰め込みます。容器の底では、パッチ粒子がすし詰め状態 (密充填) となっています。上部にいくほど隙間が広がって密度が下がり、上澄み液ではパッチ粒子がクラスターを作って分散します。このようにして、一度の実験によって密充填から分散状態までのさまざまな密度におけるパッチ粒子系を観測することができます。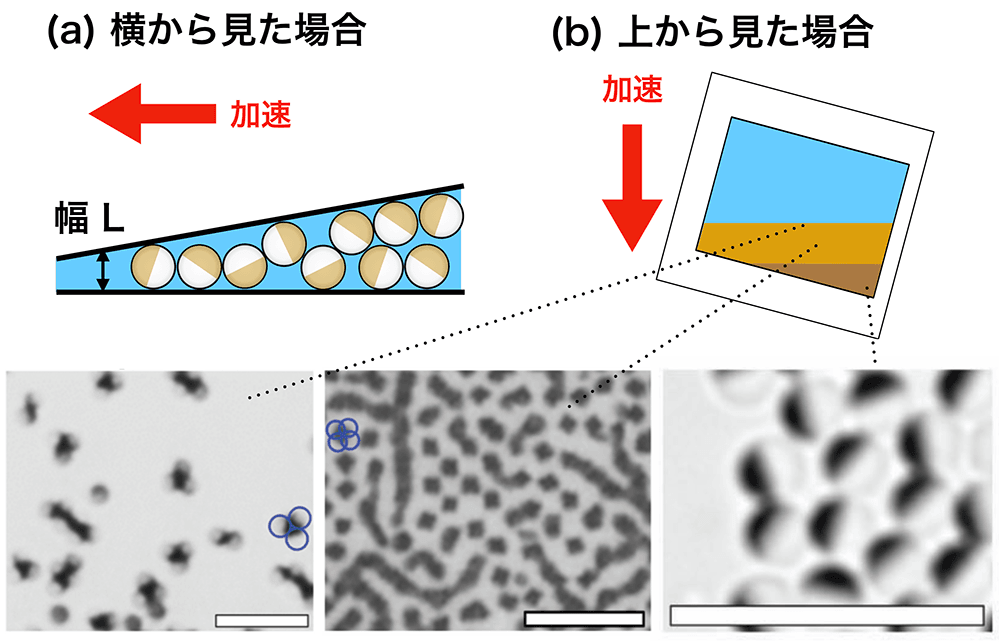

パッチ面を見る

パッチの向きを光学顕微鏡 “optical microscope” で観測します。観測結果の例を (図6) の下部に載せています。黒く写っているものが金パッチで、薄ぼんやりと写っているものがシリカ粒子です。このように、数 ㎛² しかない微小なパッチ面をハッキリと捉えることができます。

実験の結果 (密充填の場合)

まずは密充填における実験結果を見ていきます。パッチ粒子は突起を持った形状をしているため、密充填においてはパッチ粒子の回転運動が「凍結」すると考えられます。このような状況でパッチの向きに秩序は現れるのでしょうか ?

実際に観測すると 図7 のような方向秩序やクラスターが現れました。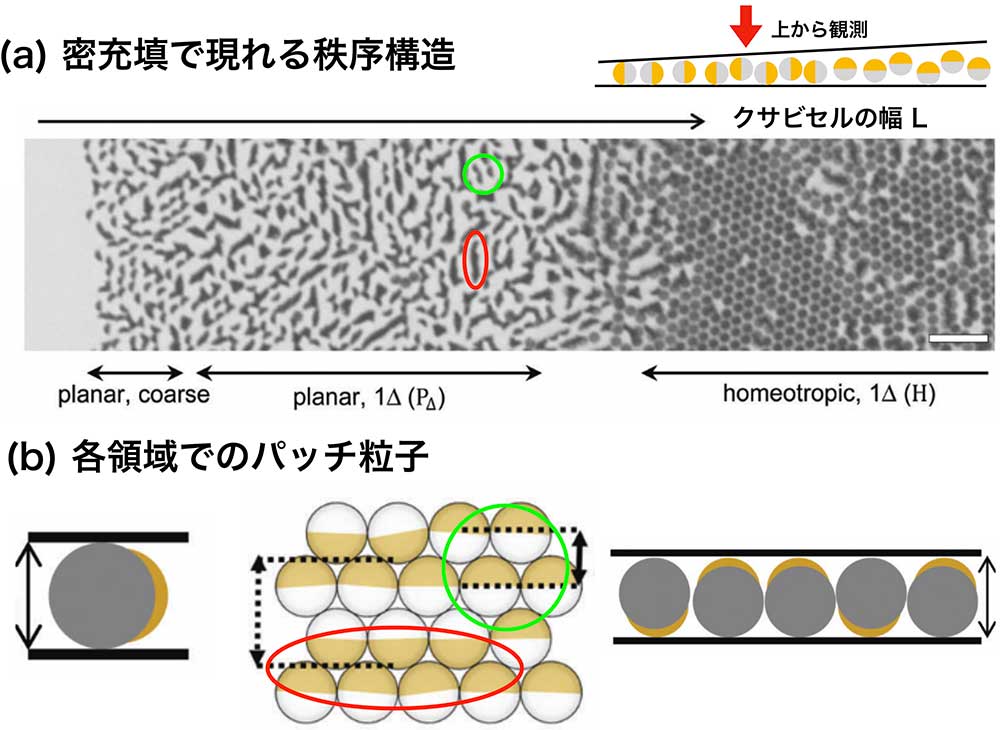

幅Lが狭い「planar, coarse 領域」と「planar, 1△ 領域」ではパッチ面が水平を向いていますが、幅Lが大きな「homeotropic, 1△ 領域」では垂直を向くようになります。また、「planar, 1△ 領域」でのみ直線形クラスターが現れており、その向きや長さはランダムに見えます。これらの方向秩序やクラスターはどのようなメカニズムで形成されたのでしょうか ?

方向秩序と形状の異方性

実は、形状の異方性 (パッチの厚み) が方向秩序を支配しています。図7 (b) にあるように、「planar, coarse 領域」と「planar, 1△ 領域」では、クサビセルの幅Lがパッチ粒子の長軸よりも短く、パッチ粒子が横向きでしか収まることができません。そのため、パッチは面内配向 “planar alignment” を示します。「homeotropic, 1△ 領域」では、幅Lが長軸よりも長くなっており、パッチ粒子が縦にも収まります。できるだけパッチ粒子を接触させたほうが高密度になるため、密充填では垂直配向 “homeotropic alignment” が実現します。

二本鎖クラスターはいつ形成されたか

「planar, 1△ 領域」でのクラスター形成はどのように理解されるのでしょうか。クラスターの大部分がパッチを向かい合わせた二本鎖クラスターであることから、パッチ間引力がクラスター形成を促しているように見えます。しかし、密充填では回転運動が「凍結」しているため、パッチ間引力があってもパッチを揃えることはできません。したがって、密に充填される前にパッチが結合していると予想できます。実際にパッチ粒子の分散系を観測したところ、パッチ粒子が離合集散しながら四面体形クラスターを作っていました (図6, 左下の写真)。この動的な四面体形クラスターが密に詰め込まれることで、パッチ間引力の履歴を残した 2 本鎖クラスターが形成されたのです。

相互作用の異方性 vs. 形状の異方性

パッチサイズ θ_ap を変えて同じ実験をおこない、相互作用の異方性と方向秩序との関係を調べました。クラスターの模様がぼやけたりするものの、基本的な構造は変わりませんでした。したがって、密充填においては「相互作用の異方性」が本質的ではなく、「形状の異方性 (パッチの厚さ)」はわずかであっても方向秩序を劇的に変えることが明らかとなりました。

実験の結果 (ゆるく詰めた場合)

次に、ゆるく詰めた場合の方向秩序を調べます。密充填にくらべて粒子間隔が広いため、パッチ粒子が自由に回転できるようになり、パッチ間引力で方向秩序が現れると予想できます。

実験の結果を 図8 (b1,b2,b3) に示します。ここではクサビセルの幅が粒子 2 個程となる部分に着目しています。密度が低くなるにしたがって、パッチ粒子の巨大な塊が小さなクラスターへと分かれる様子を見て取れます。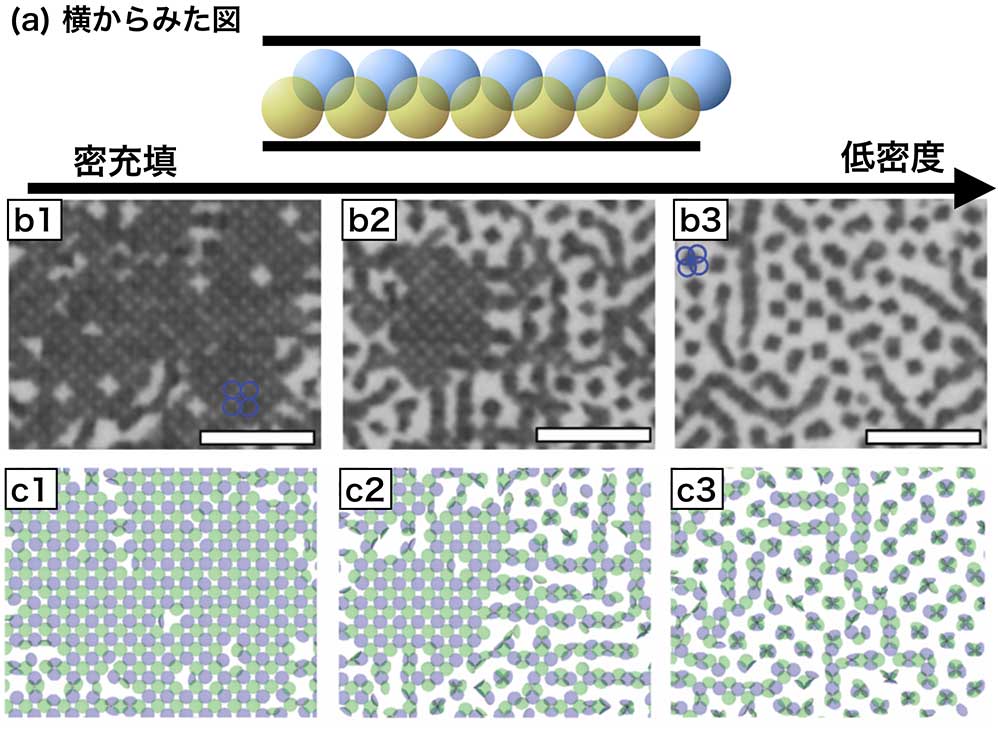

密充填となる 図8 (b1) では二層構造 (BL_□ 構造) が現れます。上下層のそれぞれで正方格子の配置をとっています。パッチ面は垂直配向を示しており、上層と下層でパッチ面が向かい合わせになっています。密度を小さくしていくと正方格子の一部がくずれて直線形・四面体形クラスターが現れはじめます (図8 (b2))。さらに低密度では直線形クラスターが消失し、四面体形クラスター構造 (T 構造) が大部分を占めるようになります (図8 (b3))。

数値シミュレーションの結果と比較

モンテカルロ法による数値シミュレーションの結果を 図8 (c1,c2,c3) に示します。計算の結果は「密充填における BL_□ 構造」や「低密度における直線形クラスターや T 構造」を示しており、実験で得られた特徴を見事に捉えています。数値シミュレーションではパッチの厚みを無視して、パッチ粒子が自由に回転できると仮定しています。このような簡単化をしても実験結果を再現するということは、低密度では形状の異方性が重要ではなく、回転運動とパッチ間引力の競合によって方向秩序が生み出されることを示唆しています。このことは岩下助教らによる過去の研究成果 “ ” ^[4]とも一致しています。

方向秩序はなぜ密度変化するのか

密度を細かく変えた数値シミュレーションをおこなったところ、密充填から 1% ほど密度を下げた途端にBL_□ 構造から T 構造へと平衡化することが分かりました。この結果は一見すると不思議に見えます。自由に回転しているパッチ粒子系に対して密度を下げたところで、回転運動にはほとんど影響せず、急激な平衡化を生み出さないように思えるからです。

そこで岩下助教らは、「引力によるエネルギー」と「回転・並進運動エントロピー」について考察し、BL_□ 構造と T 構造の安定性を議論しました: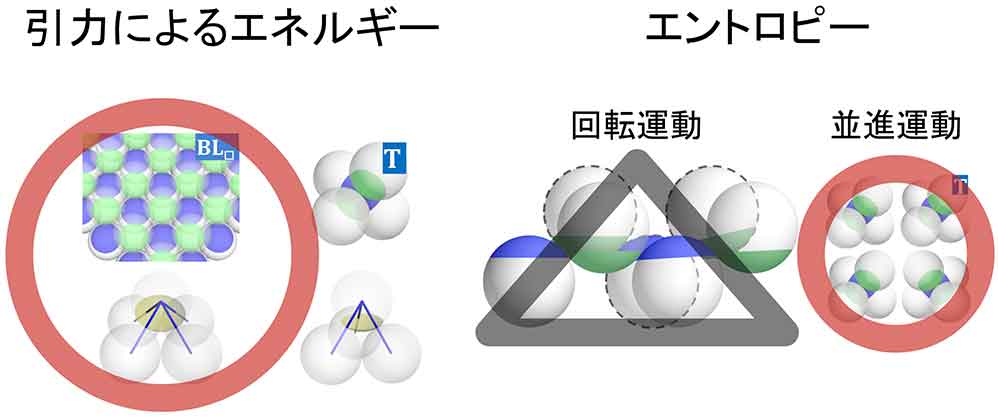

1. 引力によるエネルギー (BL_□ > T, 密度によらない)
   　パッチ間には引力がはたらくので、一つのパッチに多くのパッチが付くほどエネルギー的に安定となります。BL_□ 構造では平均して 4 個のパッチ粒子が付き、T 構造では平均して 3 個のパッチ粒子が付きます (図9, 左図)。したがって、引力だけを考えれば BL_□ 構造の方が安定です。
2. 並進運動のエントロピー (BL_□ < T, 密度に強く影響される)
   　常温で氷が水になるように、自然はより乱雑な状態 (エントロピーが大きな状態) を好みます。BL_□ 構造は言うなれば平面状の巨大なクラスターであるため、並進運動のエントロピーをあまり稼げません。一方、T 構造における四面体クラスターは、それぞれが並進運動して様々な配置をとることができて BL_□ 構造よりも多くのエントロピーを稼ぐことができます (図9, 右図)。密度を小さくすると粒子の移動範囲が広がるため、両者の並進エントロピー差はどんどん大きくなります。
3. 回転運動のエントロピー (BL_□ < T, 密度に弱く影響される)
   　BL_□ 構造や T 構造ではパッチ間にボンドができるため、パッチ粒子に許されるのは回転軸周りにゆらぐ運動となります。BL_□ 構造では正方格子配置を保ったまま密度を下げなければならないため、パッチ面間の相対角度が小さくなり、軸周りのゆらぎが抑制されます (図9, 右図)。したがって、密度を下げると BL_□ 構造における回転運動のエントロピーは減少します。

以上のように、二次元的に閉じ込められたパッチ粒子が引力で結びついていると、パッチ粒子が球形であっても並進運動エントロピーと回転運動エントロピーに結合が現れます。この結合によってBL_□ 構造が不安定化して、より安定な構造である T 構造へと変化することが分かりました。従来の 1 パッチ粒子の研究では、粒子の回転運動に注目することがほとんどでした。しかしながら、平衡化した方向秩序を実験的に見るためには、回転運動と並進運動の結合も無視できないことが本研究により初めて示唆されました。

まとめと今後の展望

さまざまな密度における 1 パッチ粒子系を観測し、凝縮構造が生みだされるメカニズムの一端を解明しました。秩序化のメカニズムは密度によって異なっており、密充填では形状の異方性からくる剛体的な相互作用に支配されていました。また低密度になると形状の異方性は効かなくなり、パッチ粒子の回転運動とパッチ間引力の競合によって方向秩序が生み出されていました。さらに、密度減少にともなう急激な秩序化は、並進運動と回転運動の結合によって誘起されることが明らかとなりました。

本研究では「空間的に閉じ込められた」異方的コロイド粒子系の自己組織化を調べましたが、このような状況はありとあらゆる系で実現します。たとえば、生体システムにおけるタンパク質はせまい領域に区分けされていたり、膜状に閉じ込められたりします。こういったメゾシステムの広範な領域で見つかっている自己組織的な構造形成を理解するにあたって、本研究で明らかにした「コロイド粒子の異方性がもつ協働的・競合的な役割」が寄与するのではないかと期待されます。

本稿では実験結果のほんの一部しかご紹介できませんでした。論文にはさらに多彩で面白い構造が示されているので、興味のある方はぜひご覧ください。