九州大学 理学研究院 理学府 理学部

逆数を無限に足したときの不思議な性質

自然数1, 2, 3, 4, 5, ...の逆数、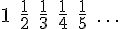

を無限に足していくと、その値は限りなく大きくなっていく。しかし自然数をそれぞれ2乗した数1, 4, 9, 16, 25, ...の逆数、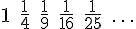

を無限に足していくと、ある値に収束することが知られている。これはバーゼル問題と呼ばれ、π²/6に収束することを1735年にオイラーが示した。さらに、自然数を3乗した数や4乗した数、それ以上の累乗数の逆数を無限に足した場合も収束することがわかっている。このように自然数をk乗した数の逆数を無限に足した値は、リーマンゼータ値と呼ばれる（図1）。

リーマンゼータ値と多重ゼータ値

このリーマンゼータ値は、素数分布などと深い関わり合いがあり、非常に古くから研究が行われてきた。その中でこのリーマンゼータ値の拡張のひとつとして、自然数の累乗数を複数掛け合わせたものの逆数とする対象が提示された。これを多重ゼータ値と呼ぶ（図1）。

多重ゼータ値の巡回和とは？

近年になって、多重ゼータ値は結び目理論やガロア理論、量子物理などさまざまな分野と結びつく重要な研究分野であることが明らかになってきた。そこで、多重ゼータ値の性質を調べる研究が盛んに行われている。そのなかでも、多重ゼータ値同士の間に多くの関係式が成り立つことに注目が集まっている。以下のような巡回和公式もそんな関係式のひとつである（図2）。

巡回和公式の証明には、特殊な技法が必要だった。

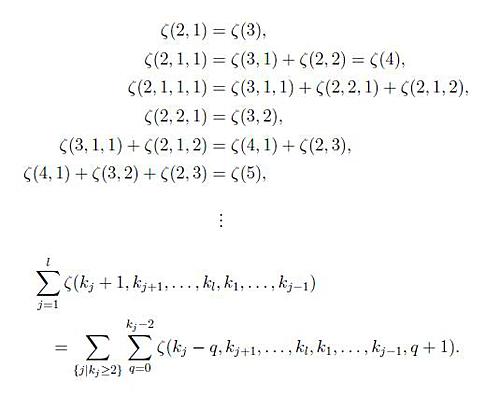
巡回和公式とは、あらかじめ固定しておいた多重ゼータ値k₁, k₂, ..., k_lをある種“巡回”させた多重ゼータ値の2通りの和が等しいという等式である。この巡回和公式は、ある特殊な級数を用いて部分分数分解を駆使すれば証明できるのだが、その証明方法以外には知られていなかった。部分分数分解が適用できる空間ではこの証明方法でよいが、それが適用できない空間で定義される多重ゼータ値（たとえばp進多重ゼータ値など）に対しては、この証明方法は使えないといった問題があった。

巡回和公式の、普遍的な証明に成功した。

そこで数理学研究院の田中さんは、若林徳子氏（九州産業大学講師）と共同で、巡回和公式の普遍的な証明に取り組んだ。そして巡回和公式を代数的に記述することで、多重ゼータ値間の関係式として既に知られている川島関係式に帰着することを証明した。既知の川島関係式に帰着する田中さんらの証明により、多重ゼータ値同士の間で川島関係式がなりたっていることが示せば、巡回和公式も成り立つことを示せることとなった。

田中さんは、「この代数的な記述により、巡回和公式は、“導分関係式”、“ポアソン代数”などとのより深い関わり合いやその他代数的な拡張も期待できる。」と語る。