

素数は数の性質を考える上でとても重要だが、実はどのような数の集合の中で考えるかで素数であるかないかが変わってしまう。数理学府の吉田さんは、素数が素数でなくなる度合いを表す手法の1つを洗練し、より正確な度合いの測定を可能にした。
素数とは、2, 3, 5, 7 ...とつづく「それを割り切る数が2個しかない自然数」のことである。例えば7は1と7でしか割れない。この「割り切る数が2個しかない」という性質は、整数全体の集合{..., −3, −2, −1, 0, 1, 2, 3, ...}で見たときには成り立つが、もう少し大きい数の集合を考えたときは、その集合の別の素数で割り切れてしまうことがある。
素数2の場合、整数全体の集合では1と2でしか割り切れない。しかし、虚数iを含む集合を考えたとき、
2 = (i − 1)(i − 1)i
というように、i − 1で割り切れてしまう。(虚数iとは2乗して−1になる数。i2 = −1)。2は虚数iを含む集合を考えたとき、素数ではなくなってしまう。これを「2は虚数iを含む集合で分岐する[1]」という。
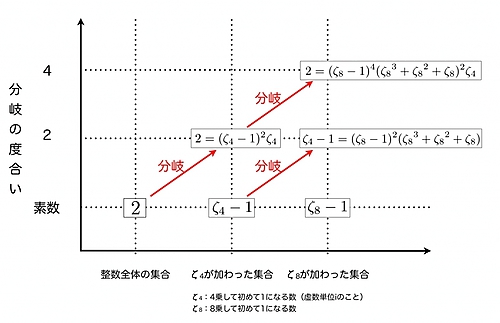
いま2という数はi − 1で2回割り切れているので、分岐の度合い2だけ素数から遠ざかったと考える。さらに別な数の集合を考えると、さらに分岐の度合いが増して素数から遠ざかることがある。今回の吉田さんの研究は、素数に関して重要な役割を果たすガロア表現での分岐の度合いに関するものだ。非常に難解なガロア表現による分岐の度合いだが、Fontaineという研究者が、(Pm)と呼ばれる条件によって分かりやすく示した。吉田さんは、Fontaineの条件(Pm)をさらに洗練し、より正確な素数分岐の度合いの測定を可能にした。

ガロア表現とは、有名なフェルマーの最終定理を証明する上でも重要となり、素数研究においても大切な役割を果たす考え方で、ごく簡単に言うと「方程式の解同士の関係を上手く行列として表現したもの」である。ガロア表現での分岐の度合いは専門家にとっても非常に難解であるが、Fontaineの研究をふまえた吉田さんの研究によって、より正確な測定が可能になった。今後この研究成果は、数の性質を調べる上で重要な素数分岐の研究で重要なツールとなるだろう。
Note:
より詳しく知りたい方は・・・