JAPANESE

HOME  /  Departments  /  Physics  /   Statistical Physics

Statistical Physics

  • NOMURA Kiyohide, Associate Professor
Theoretical study of statistical physics and condensed matter, and related topics. Subjects include, but are not limited to,
  1. field theoretical approach of low dimensional quantum systems of spins and electrons.
  2. critical phenomena and nonlinear susceptibility.

Shear thickening in granular-fluid mixture:

Figure 1. Dilatant fluid in theTaylor-Couette cell: The thickened regions are colored as red (compressive) and blue (tensile).

Dense granule-fluid mixture is called dilatant fluid and often shows severe shear thickening; its viscosity discontinuously increases by orders of magnitude under shear stress. We have developed a phenomenological model for its macroscopic behavior and found that the medium may show shear thickening oscillation, namely, the oscillation between thickened and relaxed states under a constant external state in a certain range[1]. This oscillation had never been reported, thus we constructed a experimental setup for this purpose and demonstrated the medium actually shows the oscillation as we predicted[2]. We also demonstrated that the thickening appear in the region of tensile stress[3].

[1] H. Nakanishi, S. Nagahiro, and N. Mitarai, Phys. Rev. E 85, 011401 (2012).
[2] S. Nagahiro, H. Nakanishi and N. Mitarai, EPL 104 (2013) 28002.
[3] S. Nagahiro and H. Nakanishi, submitted. arXiv:1511.05250

Non-equilibrium dynamics of single polymers:

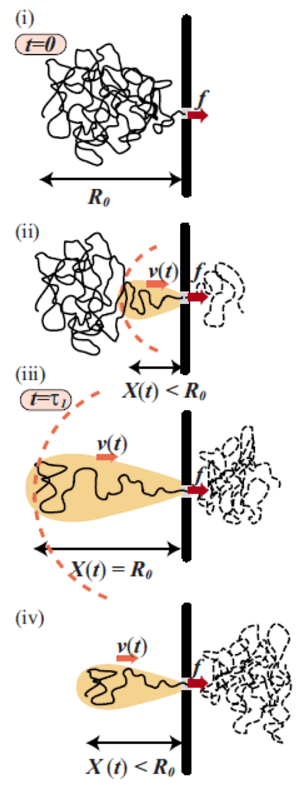
Figure 2. Illustration of the non-equilibrium process of polymer translocation.

We study the dynamic of a long flexible polymer driven by various external forces. A key example is the translocation of biopolymers, i.e., the threading of DNA, RNA and proteins through a narrow pore. We have pointed out that in typical experiments, the translocation process takes place in the condition far-from-equilibrium accompanying of large conformational distortion (Fig. 1). We elucidated the underlying physics in term of the tension propagation along the chain backbone, and constructed a basic framework to describe such a highly non-equilibrium process [1].

The concept of tension propagation is important in various problems in polymer dynamics, including a stretching process by tensile force [2] and a rotation around a bar driven by torque [3]. A conceptually similar dynamics can be seen in the compression dynamics of nano-channel confined DNA, where the stress propagation manifests itself as the development of concentration shock wave [4].

[1] T. Sakaue, Phys. Rev. E. vol. 76 (2007) 021803; ibid, vol. 81 (2010) 041808.
[2] T. Sakaue. T. Saito and H. Wada, Phys. Rev. E. vol. 86 (2012) 011804.
[3] M. Laleman et al., Macromolecules. vol. 49 (2016) 405.
[4] A. Khorshid et al. Phys. Rev. Lett. vol. 113 (2014) 268104.