


格子暗号は次世代国際標準暗号の有力候補です。その安全性評価のため2016年6月にスタートした暗号解読コンテストで、九州大学マス・フォア・インダストリ研究所先進暗号数理デザイン室(高木剛教授)とKDDI研究所の研究チームが世界で初めて60次元の格子暗号問題を解読しました。総当たり方式ならば解読までに一万年以上かかる問題を、効率的な手法により約16日で解くことに成功しました。本成果はコンピュータセキュリティシンポジウム2016(2016年10月、秋田)などで発表されました。
暗号の歴史は古く、ローマ時代にはシーザー(カエサル)が暗号を使っていたという記録が残っています(図1)。

暗号文を解読する際にも、暗号のアルゴリズム(暗号化と復元の手順)を開発する際にも、数学者が活躍します。第二次世界大戦時にはイギリスの数学者チューリングを中心としたチームが、エニグマと呼ばれるドイツ軍の暗号を効率的に解読する手法を開発しました。また、シーザー暗号やエニグマを含む旧来の暗号は共有鍵方式と呼ばれ、暗号通信をする前に送受信者ペアの間で鍵となる数字(図1の例では「13」)を決めておかねばなりません。この方式ではペアごとにひとつの鍵数字が必要なので多くの相手と通信する人は鍵の管理が大変ですし、より重大なことに、元々離れたところにいるペアが事前に鍵数字を決める際の通信を暗号化できないという問題があります。1976年に数学者ディフィーとヘルマンが、2種類の鍵数字(暗号化専用の公開鍵・復元専用の秘密鍵)を使い分けることでこのような不都合を解消する公開鍵方式[1]を発表し、暗号の世界に革新をもたらしました。
暗号は上記のエニグマの例のように近年までは軍事など特別な分野でだけ使われるものでした[2]が、インターネットや無線通信の普及とともに私達の生活の中でも使われるようになりました。これら公共性の高い通信網は便利な半面、第三者が比較的簡単に通信内容を覗くことができてしまいます。そこで機密性の高い情報は送信者のPC・スマホやサーバーで暗号化されてから送られます。クレジットカード決済のオンラインショッピングも自宅外からの家電操作も、信頼できる暗号技術がなければ実用化されていなかったかもしれません。
実はアルゴリズムがわかっていれば、十分な時間と労力をかけることで暗号は必ず解読できます。図1のごく簡単なシーザー暗号の場合、鍵数字の候補は25個しかなく、それらを総当たり方式でひとつずつ試せばいつか正解に辿り着きます。ただし現代的な暗号では鍵数字の候補は理論上無限に存在し、また実際に選んだ鍵数字の桁数が大きいほど解読までにかかる期待時間が長くなります。世界最速のスーパーコンピューターを使っても解読に1年かかる難易度ならば、実用上安全と言えるでしょう。
では鍵数字を何桁以上にすれば実用上安全なのでしょうか。この桁数は最速スパコンの性能によって決まり、計算機性能は年々向上しています(図2の□印や▵印)から、必要桁数も年々増加していくことになります。計算機性能がこれからもこれまでと同じペースで向上していく(図2の右肩上がり破線)という前提のもと現在最も一般的なRSA暗号の安全性を試算したところ、広く使われてきた1024ビット(2進法で1024桁、10進法で約300桁)の鍵数字は2015年時点で既に不安で、1536ビット(10進法で約450桁)でも2035年頃には不安になると推定されました(図2の、右肩上がり破線と水平破線の交点)。現在は暫定的に2048ビット(10進法で約600桁)の鍵数字を使うことが推奨されています。
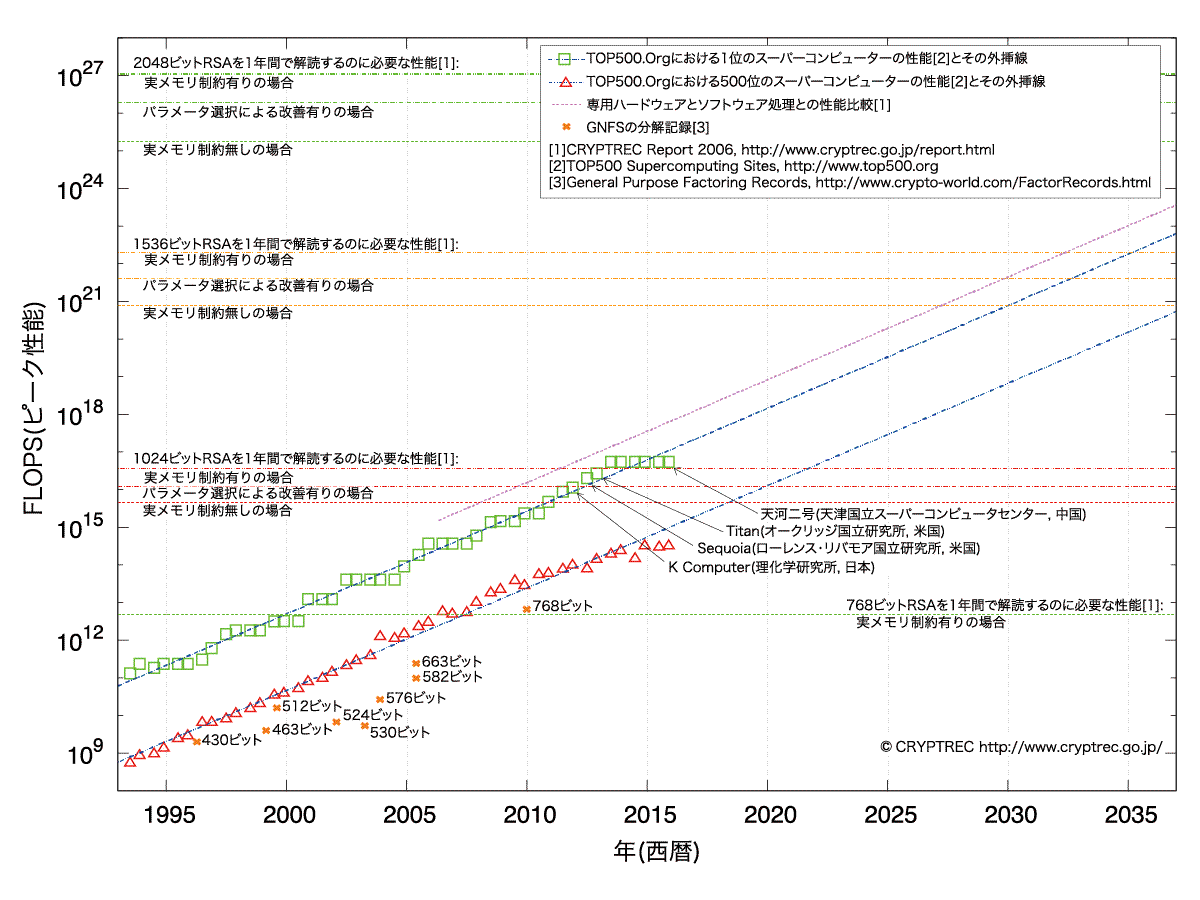

もうひとつ重要なのが解読手法です。安全性評価の際には、攻撃者が標的とする暗号アルゴリズムの性質を巧妙に利用し、総当たり方式と比べて桁違いに少ない計算量・短い時間で暗号解読する手法を使ってくると想定したほうがよいでしょう。特に新しく提案されたばかりのアルゴリズムに関しては、実はまだ誰も気づいていない大きな弱点があって鍵数字桁数にほとんど関係なく極めて短時間で解読されてしまう可能性もあるので、慎重な検討が必要です。
そこで、実用化が期待される新しい暗号方式に対して、その安全性を厳密に評価するために、ある程度の桁数の鍵数字を用いた暗号の解読コンテストが開催されています。コンテスト主催団体のホームページで問題が発表された瞬間から世界中の数学者・暗号学者が、自分たちのチームがもつ解読技術でどれだけ早く問題を解けるか競うのです。図2にはRSA暗号解読コンテストの記録(×印)と、同コンテストで多くの記録を打ち立てた効率的手法である一般数体ふるい法を攻撃者が用いると想定した場合の試算(水平破線)が示されています。
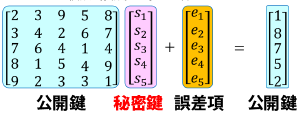
2016年6月、格子暗号という新しい暗号方式の安全性評価のためのコンテスト[3]が開催されました。現在標準的なRSA暗号や楕円曲線暗号は量子コンピューターを使うと飛躍的短時間で解読できる[4]ことが理論上わかっており、実際に量子コンピューターが開発されてしまったため図2の試算の前提がくつがえされてしまい、新しい暗号方式への速やかな移行が求められています。量子コンピューターを使っても難易度が変わらない耐量子計算機アルゴリズムがいくつか提案されてきた中で、次世代の国際標準になる可能性が高いのが格子暗号です。格子暗号は、秘密鍵から公開鍵を計算する際に意図的に誤差項(小さなノイズ)を混入させます。人工知能に画像を認識させる研究で特に難しいのがノイズを含む画像の認識なのですが、これを逆手に取り、ノイズを混入させることで秘密鍵割り出しの計算を困難にしたのです。格子暗号で鍵として使われるのはベクトル(複数の数字のセット)で、解読難易度を上げるためにはひとつの数字の桁数を大きくする代わりにベクトルの次元数(含まれる数字の個数)を大きくします。
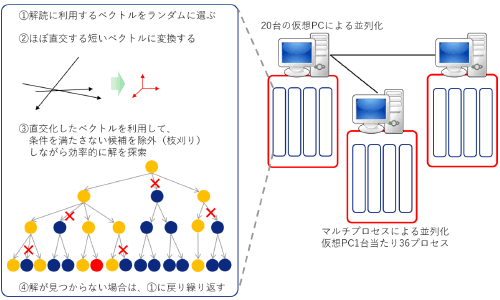
研究チームは、問題公開直後から秘密鍵ベクトルの割り出しを始めました。総当たり方式は全ての鍵ベクトル候補をいちいち最後まで試すので時間がかかります。そこで、見込みのない候補ばかりが属するグループを特定してそれらの計算を早々に切り捨て、可能性の高い候補の計算に注力するのが効率的と考えられます。この切り捨てを20台の仮想PCを並列化して作った解読システムに巧みに実装することで(図4)、総当たり方式では1万年以上かかると見積もられる60次元暗号問題を、約16日で解くことに成功しました。
60次元暗号問題が解かれたからといって格子暗号が危険というわけではありません。研究チームは並行して55次元以下の問題にも挑戦・解読しており、次元数が大きくなるほど解読時間が順当に長くなることを確認しています。 60次元を16日で解読という今回の記録は、実用上安全な格子暗号の鍵ベクトル次元数を的確に見積もるために使われるのです。
60次元を16日で解読という今回の記録は、実用上安全な格子暗号の鍵ベクトル次元数を的確に見積もるために使われるのです。
ポスト量子暗号学会議(Post-quantum cryptography conference)は2006年から1~2年間隔で開催されている国際学術会議です。今年(2016年)は高木教授らが実行委員となり、2月に福岡市の九州大学西新プラザで開催されました。この福岡会議でアメリカ国家安全保障局(NSA)とアメリカ国立標準技術研究所(NIST)の代表職員が重大プランを発表するという告知がなされ、会議参加者数は前年度の倍以上となりました。当日は両組織のRSA暗号から新暗号への移行計画案が発表され、この案に対する質問・コメントが求められました。出席者の中にはtwitterを使って会場外(世界中の人々)から募った質問を代理でNSA/NIST代表にぶつける人もいて、活発な質疑応答がなされました。
Note:
より詳しく知りたい方は・・・