
HOME / Departments / Physics / Condensed Matter Theory
Condensed Matter Theory
-
- FUKUDA Jun-ichi, Professor
- HIGUCHI Yuji◇, Associate Professor
- MATSUI Jun, Lecturer
- TARAMA Mitsusuke, Assistant Professor
- ◇ Research Institute for Information Technology
- Research topics in our group cover various phenomena in non-equilibrium systems and complex systems. Our focus is on theoretical and computational physics of soft condensed matter, and current research subjects include:
- Self-organized structures and dynamics of liquid crystals
- Optical properties of ordered structures in soft matter
- Field theory of polymeric systems
- Poly-amorphism and crystallization
- Slowing dynamics near the glass transition
- Dynamics of active matter
- Non-equilibrium physics of biological and living matter
- Water dynamics
- Structures and physical properties of polymer
1. Self-organized structures and dynamics of liquid crystals
We study various self-organized structures and dynamics of liquid crystals, mainly by numerical calculations based on continuum theories. Research topics of interest include, but are not limited to, exotic phases known as cholesteric blue phases [1], liquid crystal colloids (in part collaboration with Prof. Yasuyuki Kimura in our Department) [2], and liquid crystals in contact with sinusoidal grooves [3]. The structure of topological defects in liquid crystals is a major subject of interest.
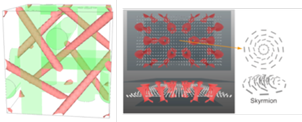
References:
[1] Fukuda and Takahashi, PNAS 121, e2412476121 (2024); Fukuda Liq. Cryst. Rev. 10, 69 (2022); Yamashita and Fukuda, Phys. Rev. E 105, 044707 (2022); Fukuda and Žumer, Phys. Rev. Lett. 104, 017801 (2010); Phys. Rev. Lett. 106, 097801 (2011); Nature Commun. 2, 246 (2011)
[2] Fukuda, J. Phys. Soc. Jpn. 78, 041003 (2009); Fukuda and Yokoyama, Phys. Rev. Lett. 94, 148301 (2005); Fukuda et al., Phys. Rev. E 69, 041706 (2004)
[3] Ohzono, Yamamoto and Fukuda, Nature Commun. 5, 3735 (2014); Ohzono and Fukuda, Nature Commun. 3, 701 (2012)
2. Optical properties of ordered structures in soft matter
Soft materials often exhibit self-organized structures whose periodicity is of the order of the wavelength of visible light. We investigate the properties of such structures as photonic crystals, and also how they can be observed by optical means such as confocal microscopy.

References:
Fukuda et al., Ann. Phys. 534, 2100336 (2022); Fukuda et al., Sci. Rep. 8, 17234 (2018); Nych, Fukuda et al., Nature Phys. 13, 1215 (2017); Fukuda et al., Proc. SPIE 10555, 105550A (2018); Proc. SPIE 9769, 976906 (2016)
3. Field theory of polymeric systems
From a microscopic model of semiflexible chains with bending elasticity, we made use of a field theory to derive the free energy functional and the equations of motion for compositional and orientational order parameters of the polymer component. We studied the coupling between phase separation and orientational ordering in the time evolution of these two order parameters.

References:
Fukuda and Yokoyama, J. Phys. Soc. Jpn. 71, 1463 (2002); J. Chem. Phys. 115, 4930 (2001); Fukuda, Phys. Rev. E 59, 3275 (1999); Phys. Rev. E 58, 6939 (1998); Eur. Phys. J. B 7, 573 (1999)
4. Poly-amorphism and crystallization
We are interested in a model monatomic system, which is crystallized under cooling at high pressure and vitrified under cooling at low pressure. Using molecular dynamics simulation, we are calculating the T-P diagram and exploring the border between glass and crystalline in middle range of pressure.

5. Slowing dynamics near the glass transition
We aim to understand the glass transition at the microscopic point of view; molecules are mostly trapped in cages formed by their surrounding molecules, which cause the diffusion coefficient decreasing and anomalous in highly supercooled liquids. Occasionally molecules hop to the neighbor's site and the neighbor do in the same way. These motions are collective and intermittent.
References:
T. Muranaka, J. Matsui and Y. Hiwatari, Mol. Sim. 41, 10-12, 822 (2015).
6. Dynamics of active matter
Active matter refers to an object, or a group of them, that undergoes spontaneous motion even without external forcing. Examples include biological systems such as moving cells and molecular motors as well as synthetic ones such as active colloids and self-propelled droplets. We are developing theory to understand the rich dynamics that active matter exhibits due to its internal degrees of freedom.We are also studying model systems of bacterial suspensions, particularly focusing on their behavior under spatial confinement.
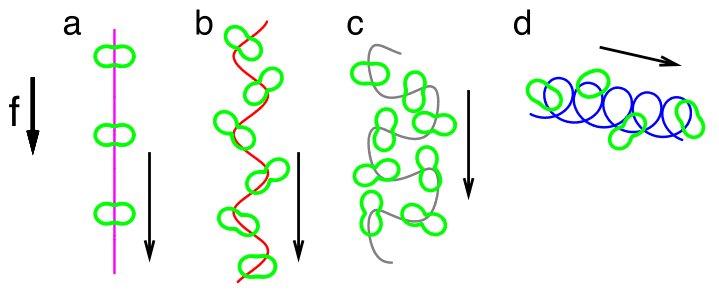
References:
M. Tarama, Phys. Rev. E 96, 022602 (2017); J. Phys. Soc. Jpn. 86, 101011 (2017); "Self-organized Motion: Physicochemical Design based on Nonlinear Dynamics”, Chapter 12. "Nonlinear Dynamics of Active Deformable Particles” (S. Nakata, et al. eds.), RSC e-book (2019).
M. Tarama and T. Ohta, Europhys. Lett. 114, 30002 (2016).
T. Ohta, M. Tarama, and M. Sano, Physica D 318-319, 3-11 (2016).
H. Matsukiyo and J. Fukuda, Phys. Rev. E 109, 0546406 (2024)
7. Non-equilibrium physics of biological and living matter
Biological living cells exhibit various dynamics because of their intracellular force generation. We aim to understand the dynamics of living cells and the underlying mechanism from the viewpoint of nonequilibrium physics. Our research projects include the dynamics and mechanics of cytoskeleton, i.e., intracellular force generating molecules that drive the dynamics of cells, as well as the migration of individual living cells and their collective motion, which are of essential importance in many biological processes including development.

References:
M. Tarama and R. Yamamoto, J. Phys. Soc. Jpn. 87, 044803 (2018).
M. Tarama, K. Mori, and R. Yamamoto, Front. Cell Dev. Biol. 10, 1046053 (2022).
M. Tarama and T. Shibata, Phys. Rev. Research 4, 043071 (2022).
S. Sekine, M. Tarama, et al. Nat. Commun. 15:464 (2024).
8. Water dynamics
The structure and dynamics of water are interesting objects in physics and chemistry. Furthermore, the dynamics of water molecules around soft matter affect the self-organized structure of soft matter, the biocompatibility of biomaterials, and the biological functions, and therefore are interesting and significant subjects. We study water dynamics around soft matter by molecular simulations.

References:
M. A. Saleh, Y. Higuchi, S. Shiomoto, T. Anada, M. Hishida, and M. Tanaka, Polym. J. 57, 1127–1139 (2025).
Y. Higuchi, M. A. Saleh, T. Anada, M. Tanaka, and M. Hishida, J. Phys. Chem. B 128, 5008–5017 (2024).
Y. Higuchi, Y. Asano, T. Kuwahara, and M. Hishida, Langmuir 37, 5329–5338 (2021).
9. Structures and physical properties of polymer
Polymer forms complex structures, such as hierarchical structures and network structures. Therefore, elucidating the correlation between structure and physical properties is difficult but interesting. As an example, we study the deformation and fracture process of semicrystalline polymers, gels, and elastomers by molecular dynamics simulations.

References:
Y. Higuchi, Y. Hikima, N. Kamiuchi, E. Uehara, Y. Oya, G. Yamamoto, and K. Sakakibara, Polymer 333, 128539 (2025).
D. G. Tsalikis, M. Ciobanu, C. S. Patrickios, and Y. Higuchi, Macromolecules 56, 9299–9311 (2023).
Y. Higuchi, Phys. Rev. E 103, 042502 (2021).
Y. Higuchi, K. Saito, T. Sakai, J. P. Gong, and M Kubo, Macromolecules 51, 3075–3087 (2018).
Y. Higuchi and M. Kubo, Macromolecules 50, 3690–3702 (2017).